Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
Những câu hỏi liên quan
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
15 tháng 3 2021 lúc 20:29
Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^o\) ; \(\widehat{CAD}=90^o\).
Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB và IJ.
Cho tứ diện SABC có cạnh SA vuông góc với mặt phẳng (ABC) có SA = a, AB = b, AC = c. Xác định tâm và bán kính hình cầu ngoại tiếp tứ diện trong các trường hợp sau :
a) \(\widehat{BAC}=90^0\)
b) \(\widehat{BAC}=60^0\) và b = c
c) \(\widehat{BAC}=120^0\) và b = c
cho tứ giác ABCD có 2 đường chéo cắt nhauc tại O thỏa mãn OC=2OA;\(\widehat{BOC}=60^0\).Biết rằng \(\widehat{ABD}=15^0;\widehat{CAD}=90^0\).Tính số đo các góc của tứ giác ABCD
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a. \(\widehat{BAD}=120^0;\widehat{BA'D}=90^0\). Tính thể tích hình hộp theo a ?
Cho tứ diện ABCD có AB 3, AC 2, AD 6,
B
A
C
^
90
°
,
C
A
D
^
120
°
,
B
A
D
^
...
Đọc tiếp
Cho tứ diện ABCD có AB = 3, AC = 2, AD = 6, B A C ^ = 90 ° , C A D ^ = 120 ° , B A D ^ = 60 ° . Thể tích khối tứ diện ABCD bằng
A. 6 2
B. 2 2 3
C. 2
D. 3 2
Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
Đúng 0
Bình luận (0)
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : widehat{A}+widehat{B}200^{^0};widehat{B}+widehat{C}218^0;widehat{C}+widehat{D}160^0 TÍNH widehat{C}VÀ widehat{D}BÀI 2 : CHO TỨ GIÁC ABCD CÓ widehat{B}80^0;widehat{D}120^0GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC BÀI 3 : TỨ GIÁC ABCD CÓ widehat{A}57^0;widehat{C}110^0;widehat{D}75^0.TÍNH GÓC NGOÀI TẠI ĐỈNH B
Đọc tiếp
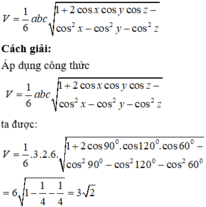
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : \(\widehat{A}+\widehat{B}=200^{^0};\widehat{B}+\widehat{C}=218^0;\widehat{C}+\widehat{D}=160^0\) TÍNH \(\widehat{C}\)VÀ \(\widehat{D}\)
BÀI 2 : CHO TỨ GIÁC ABCD CÓ \(\widehat{B}=80^0;\widehat{D}=120^0\)GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC
BÀI 3 : TỨ GIÁC ABCD CÓ \(\widehat{A}=57^0;\widehat{C}=110^0;\widehat{D}=75^0\).TÍNH GÓC NGOÀI TẠI ĐỈNH B
Cho hình thang vuông ABCD (AB // CD) có \(\widehat{A}=\widehat{D}=90^0,\widehat{B}=60^0,CD=30cm,CA\perp CB\) . Tính diện tích của hình thang ABCD.
Cho tứ giác ABCD biết \(\widehat{B}+\widehat{C}=200^0;\widehat{B}+\widehat{D}=180^0;\widehat{C}+\widehat{D}=120^0\). Tính các góc của tứ giác ABCD.
Theo đề bài, ta có: \(\widehat{B}+\widehat{C}+\widehat{B}+\widehat{D}=200^0+180^0\)
\(\Leftrightarrow2\widehat{B}+\left(\widehat{C}+\widehat{D}\right)=380^0\)
\(\Leftrightarrow2\widehat{B}=380^0-120^0=260^0\)
\(\Rightarrow\widehat{B}=130^0\Rightarrow\widehat{C}=70^0,\widehat{D}=50^0\)
Mỗi tứ giác đều được tạo thành từ \(2\) tam giác phân biệt nên tổng các góc trong một tứ giác là \(360^0\).
Do đó, \(\widehat{A}=360^0-130^0-70^0-50^0=110^0\)
Vậy: ...
( Có hết trên kia rồi, bạn tự bổ sung từ vậy )
Đúng 0
Bình luận (0)