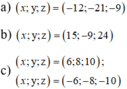Đoạn:

2x
2 + 2y
2 − 3z
2= -100 là như thế nào bạn nhỉ?

Bạn viết lại đề để mọi người hiểu hơn nhé.

Bài 1: 

Ta có: \(3x=2y\)

nên \(\dfrac{x}{2}=\dfrac{y}{3}\)

mà x+y=-15

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{-15}{5}=-3\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{2}=-3\\\dfrac{y}{3}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-9\end{matrix}\right.\)

Vậy: (x,y)=(-6;-9)

Bài 2: 

a) Ta có: \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}\)

mà x+y-z=20

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y-z}{4+3-5}=\dfrac{20}{2}=10\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{4}=10\\\dfrac{y}{3}=10\\\dfrac{z}{5}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=40\\y=30\\z=50\end{matrix}\right.\)

Vậy: (x,y,z)=(40;30;50)

Bài 2: 

b) Ta có: \(\dfrac{y}{3}=\dfrac{z}{7}\)

nên \(\dfrac{y}{12}=\dfrac{z}{28}\)

mà \(\dfrac{x}{11}=\dfrac{y}{12}\)

nên \(\dfrac{x}{11}=\dfrac{y}{12}=\dfrac{z}{28}\)

hay \(\dfrac{2x}{22}=\dfrac{y}{12}=\dfrac{z}{28}\)

mà 2x-y+z=152

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{2x}{22}=\dfrac{y}{12}=\dfrac{z}{28}=\dfrac{2x-y+z}{22-12+28}=\dfrac{152}{38}=4\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{11}=4\\\dfrac{y}{12}=4\\\dfrac{z}{28}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=44\\y=48\\z=112\end{matrix}\right.\)

Vậy: (x,y,z)=(44;48;112)

Áp dụng BĐT BSC:

\(F=\dfrac{1}{2x+y+z}+\dfrac{1}{x+2y+z}+\dfrac{1}{x+y+2z}\)

\(\le\dfrac{1}{16}\left(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)+\dfrac{1}{16}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{y}+\dfrac{1}{z}\right)+\dfrac{1}{16}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{z}\right)\)

\(=\dfrac{1}{16}\left(\dfrac{4}{x}+\dfrac{4}{y}+\dfrac{4}{z}\right)=\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=\dfrac{1}{4}.4=1\)

\(maxF=1\Leftrightarrow x=y=z=\dfrac{3}{4}\)

Giá trị lớn nhất là 3

3

\(\dfrac{x+2}{3}=\dfrac{y-5}{-4}=\dfrac{z+1}{5}\Rightarrow\dfrac{2x+4}{6}=\dfrac{3y-15}{-12}=\dfrac{z+1}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2x+4}{6}=\dfrac{3y-15}{-12}=\dfrac{z+1}{5}=\dfrac{2x+4-3y+15+z+1}{6-\left(-12\right)+5}=\dfrac{\left(2x-3y+z\right)+\left(4+15+1\right)}{23}=\dfrac{72+20}{23}=\dfrac{92}{23}=4\)

\(\dfrac{x+2}{3}=4\Rightarrow x+2=12\Rightarrow x=10\\ \dfrac{y-5}{-4}=4\Rightarrow y-5=-16\Rightarrow y=-11\\ \dfrac{z+1}{5}=4\Rightarrow z+1=20\Rightarrow z=19\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x+2}{3}=\dfrac{y-5}{-4}=\dfrac{z+1}{5}=\dfrac{2x-3y+z+4+15+1}{2\cdot3-3\cdot\left(-4\right)+5}=\dfrac{92}{23}=4\)

Do đó: x=10; y=-11; z=4

\(\dfrac{x+2}{3}=\dfrac{y-5}{-4}=\dfrac{z+1}{5}\text{ và }2x-3y+z=72\)

\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)

\(\dfrac{x+2}{3}=\dfrac{y-5}{-4}=\dfrac{z+1}{5}=\dfrac{2\left(x+2\right)-3\left(y-5\right)+z+1}{2.3-3.\left(-4\right)+5}=\dfrac{92}{23}=4\)

\(\Rightarrow\dfrac{x+2}{3}=4\Rightarrow x+2=12\Rightarrow x=10\)

\(\dfrac{y-5}{-4}=4\Rightarrow y-5=-16\Rightarrow y=-11\)

\(\dfrac{z+1}{5}=4\Rightarrow z+1=20\Rightarrow z=19\)

Lời giải:
Áp dụng BĐT Bunhiacopxky:

$\text{VT}(1^2+1^2+1^2)\geq (1+\frac{x}{y+z}+1+\frac{y}{x+z}+1+\frac{z}{x+y})^2$

$\Leftrightarrow 3\text{VT}\geq (3+\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y})^2$

$ = \left[3+\frac{x^2}{xy+xz}+\frac{y^2}{yz+yx}+\frac{z^2}{zy+zx}\right]^2$

$\geq \left[3+\frac{(x+y+z)^2}{2(xy+yz+xz)}\right]^2$

$\geq \left[3+\frac{3(xy+yz+xz)}{2(xy+yz+xz)}\right]^2=\frac{81}{4}$

$\Rightarrow \text{VT}\geq \frac{27}{4}$

Dấu "=" xảy ra khi $x=y=z>0$

Áp dụng BĐT Bunhiacopxky:

VT(12+12+12)≥(1+��+�+1+��+�+1+��+�)2VT(12+12+12)≥(1+y+zx​+1+x+zy​+1+x+yz​)2

⇔3VT≥(3+��+�+��+�+��+�)2⇔3VT≥(3+y+zx​+x+zy​+x+yz​)2

=[3+�2��+��+�2��+��+�2��+��]2=[3+xy+xzx2​+yz+yxy2​+zy+zxz2​]2

≥[3+(�+�+�)22(��+��+��)]2≥[3+2(xy+yz+xz)(x+y+z)2​]2

≥[3+3(��+��+��)2(��+��+��)]2=814≥[3+2(xy+yz+xz)3(xy+yz+xz)​]2=481​

⇒VT≥274⇒VT≥427​

Dấu "=" xảy ra khi $x=y=z>0$