cho tam giác ABC, D thuộc tia đối của tia BA ; DB = BA . gọi M là trung điểm của BC , K là giao điểm của DM và AC
chứng minh : AK = 2KC
MK = 1/4KD
Những câu hỏi liên quan
cho tam giác abc d thuộc tia đối tia ba e thuộc tia đối tia ca sao cho ce=bd cm bc<de
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) a) Chứng minh: Tam giác ABH= tam giác ACH b) Lấy điểm D trên tia đối của tia BC sao cho BD=BH, lấy E trên tia đối của tia BA sao cho BE=BA. Chứng minh: DE//AH
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
Đúng 0
Bình luận (0)
Cho tam giác ABC. Lấy điểm D thuộc tia đối tia BC sao cho BD=BA. Lấy điểm E thuộc tia đối của tia CB sao cho CE=CA. Gọi H là trung điểm của AD. Đường thẳng BH là đường gì đối với tam giác ABD
Cho tam giác ABC. Lấy điểm D thuộc tia đối tia BC sao cho BD=BA. Lấy điểm E thuộc tia đối của tia CB sao cho CE=CA. Gọi H là trung điểm của AD. Đường thẳng BH là đường gì đối với tam giác ABD
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) a) Chứng minh: Tam giác ABH= tam giác ACH b) Lấy điểm D trên tia đối của tia BC sao cho BD=BH, lấy E trên tia đối của tia BA sao cho BE=BA. Chứng minh: DE//AH Giải giúp mình với ◉‿◉
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔACH
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
Đúng 0
Bình luận (0)
23 tháng 12 2023 lúc 20:47
Cho tam giác ABC,lấy điểm D thuộc tia đối của tia AB,điểm E thuộc tia đối của tia AC sao cho ADAB và AEAC. Kẻ AH vuông góc với BC tại H kẻ AK vuông góc với DE tại K. Chứng minh a, tam giác ABC tam giác ADE b,BHDK c,ba điểm A,H,K thẳng hàngĐề khó quá nhờ mọi người giải với nha
Đọc tiếp
Cho tam giác ABC,lấy điểm D thuộc tia đối của tia AB,điểm E thuộc tia đối của tia AC sao cho AD=AB và AE=AC. Kẻ AH vuông góc với BC tại H kẻ AK vuông góc với DE tại K. Chứng minh
a, tam giác ABC =tam giác ADE
b,BH=DK
c,ba điểm A,H,K thẳng hàng
Đề khó quá nhờ mọi người giải với nha
a: Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}=\widehat{DAE}\)(hai góc đối đỉnh)
AC=AE
Do đó: ΔABC=ΔADE
b: Xét ΔAHB vuông tại H và ΔAKD vuông tại K có
AB=AD
\(\widehat{ABH}=\widehat{ADK}\)(ΔABC=ΔADE)
Do đó: ΔAHB=ΔAKD
=>BH=DK
c: Ta có: ΔAHB=ΔAKD
=>\(\widehat{HAB}=\widehat{DAK}\)
mà \(\widehat{HAB}+\widehat{HAD}=180^0\)(hai góc kề bù)
nên \(\widehat{DAK}+\widehat{DAH}=180^0\)
=>K,A,H thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại D, kẻ DE vuông góc với BC(E thuộc BC) , gọi F là giao điểm của BA và tia ED.
A) tam giác ABD= tam giác EBD
B)tam giác DFC cân
C) Gọi H là giao điểm của BD và CF. Trên tia đối của tia DF lấy điểm K sao cho DK=DF.Vẽ điểm I nằm trên đoạn thẳng CD sao cho CI=2DI.Chứng minh DH vuông góc với CF và ba điểm K,I,H thẳng hàng
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: Xét ΔBFC có
FE,CAlà đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc CF tại H
=>DH vuông góc CF tại H
mà ΔDFC cân tại D
nên H là trung điểm của FC
Xét ΔKFC có
CD là trung tuyến
CI=2/3CD
Do đó: I là trọng tâm
mà H là trung điểm của CF
nên K,I,H thẳng hàng
Đúng 0
Bình luận (0)
CHO MIK HỎI BÀI NÀY VS
Cho tam giác ABC. Lấy điểm D thuộc tia đối tia BC sao cho BD=BA . Lấy điểm E thuộc tia đối của tia CB sao cho CE=CA . Gọi H là trung điểm của AD. Đường thẳng BH là đường gì đối với tam giác ABD
cho tam giác ABC nhọn. Trên tia đối của tia BA lấy điểm D sao cho 2BD=BA. Trên tia đối của tia CA lấy điểm E sao cho 2CE=CA. Chứng minh tam giác ABC đồng dạng với tam giác ADE
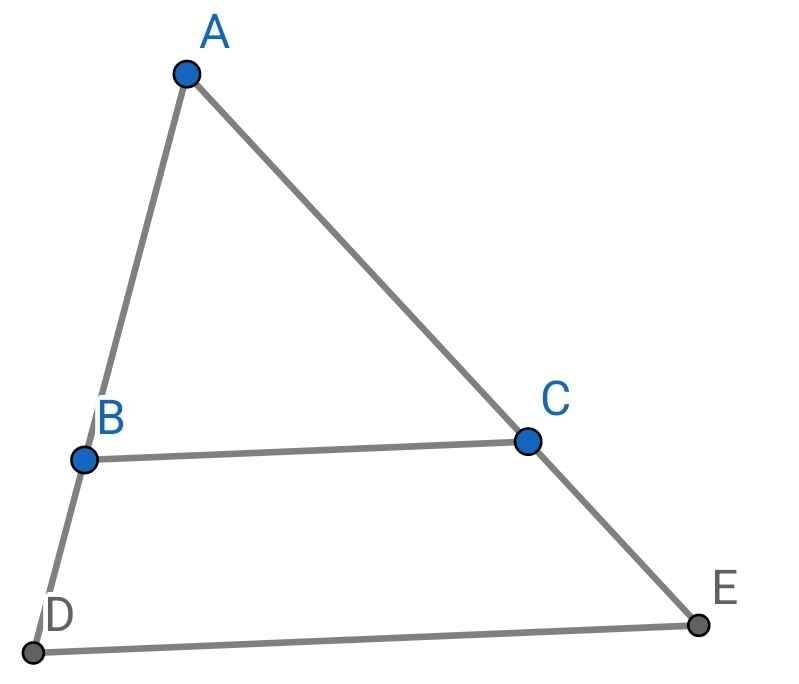Do 2BD = BA (gt)
⇒ AD = AB + BD
= 2BD + BD
= 3BD
⇒ AB/AD = 2/3 (1)
Do 2CE = CA (gt)
⇒ AE = AC + CE
= 2CE + CE
= 3CE
⇒ AC/AE = 2/3 (2)
Từ (1) và (2) ⇒ AB/AD = AC/AE = 2/3
Xét ∆ABC và ∆ADE có:
AB/AD = AC/AE (cmt)
A chung
⇒ ∆ABC ∽ ∆ADE (c-g-c)
Đúng 1
Bình luận (0)
tam giác ABC có AB=AC . Lấy D thuộc tia đối của BC , E thuộc tia đối của tia BA sao cho ED=EB .Chứng minh rằng ED//AC
( Vẽ hình zùm mik nha )