Viết phương trình tham số của đường thẳng d đi qua điểm M(-3;5) và song song với đường phân giác của góc phần tư thứ nhất

Những câu hỏi liên quan
viết phương trình tham số của đường thẳng d đi qua điểm M(2;6) và có vectơ chỉ phương \(\overrightarrow{u}\)= (2;-3)
Do d \(\left\{{}\begin{matrix}điquaM\left(2;6\right)\\vtcp\overrightarrow{u}=\left(2;-3\right)\end{matrix}\right.\)
=> Pt tham số: \(\left\{{}\begin{matrix}x=2+2t\\y=6-3t\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Viết phương trình tham số của đường thẳng d đi qua điểm M(2;3;-5) và song song với đường thẳng
∆
:
x
-
2
+
2
t
y
3
-
4
t...
Đọc tiếp
Viết phương trình tham số của đường thẳng d đi qua điểm M(2;3;-5) và song song với đường thẳng ∆ : x = - 2 + 2 t y = 3 - 4 t z = - 5 t
A. x = 2 - 2 t y = 3 + 3 t z = - 5
B. x = - 2 + 2 t y = 3 - 4 t z = - 5 - 5 t
C. x = - 2 + 2 t y = 3 - 4 t z = 5 - 5 t
D. x = 2 + 2 t y = 3 - 4 t z = - 5 - 5 t
Trong mặt phẳng Oxy cho A (4;1), B (-2;3), C (5;-1). a) Viết phương trình tham số và trình tổng quát của đường thẳng đi qua hai điểm A,C b) Viết phương trình tham số và trình tổng quát của đường thẳng A và vuông góc với B,C c) Viết phương trình tham số và trình tổng quát của đường thẳng qua A và song song với đường thẳng d : 2x - y + 3 = 0
Trong không gian Oxyz, viết phương trình tham số của đường thẳng d đi qua điểm M(1;2;-3) và d vuông góc với mặt phẳng (P): 3x + y + 1 0 A. x -1 - 3t, y -2 - t, z 3 B. x 1 + 3t, y 2 + t, z -3 + t C. x 3 + t, y 1 + 2t, z -3t D. x 1 + 3t, y 2 + t, z -3
Đọc tiếp
Trong không gian Oxyz, viết phương trình tham số của đường thẳng d đi qua điểm M(1;2;-3) và d vuông góc với mặt phẳng (P): 3x + y + 1 = 0
A. x = -1 - 3t, y = -2 - t, z = 3
B. x = 1 + 3t, y = 2 + t, z = -3 + t
C. x = 3 + t, y = 1 + 2t, z = -3t
D. x = 1 + 3t, y = 2 + t, z = -3
Đáp án D
Mặt phẳng (P) có vecto pháp tuyến là: n p → (3; 1; 0)
Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: u d → = n p → (3; 1; 0)
Phương trình tham số của đường thẳng d:
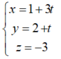
Chọn D.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0
Đúng 0
Bình luận (0)
Đường thẳng Δ có phương trình tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=-3-t\end{matrix}\right.\) và 2 điểm M(2;3), N(4;2)
Viết phương trình đường thẳng d' đi qua O biết (Δ,d')=450
Lời giải:Điểm M,N có vẻ không có vai trò gì trong bài toán.
Ta có: $\overrightarrow{u_{\Delta}}=(2,-1)$
$\overrightarrow{u_{d'}}=(a,b)$
\(\cos (\Delta, d')=\frac{\overrightarrow{u_{\Delta}}.\overrightarrow{u_d'}}{|\overrightarrow{u_{\Delta}}||\overrightarrow{u_d'}|}=\frac{2a-b}{\sqrt{a^2+b^2}.\sqrt{5}}=\cos 45^0=\frac{\sqrt{2}}{2}\)
$\Rightarrow a=3b$ hoặc $a=-\frac{b}{3}$
PTĐT $d'$ là:
$-x+3y=0$ hoặc $3x+y=0$
Đúng 0
Bình luận (1)
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;1;-3) và vuông góc với hai đường thẳng: A.
d
:
x
-
2
1
y
-
1
-
9...
Đọc tiếp
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;1;-3) và vuông góc với hai đường thẳng:
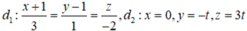
A. d : x - 2 1 = y - 1 - 9 = z + 3 - 3
B. d: x = 2 + t, y = 1 - 9t, z = -3 - 3t
C. d: x = -2 + t, y = -1 - 9t, z = 3 - 3t
D. d: x = 2 + t, y = 1 + 9t, z = -3 -3t














