Đáp án D
Mặt phẳng (P) có vecto pháp tuyến là: n p → (3; 1; 0)
Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: u d → = n p → (3; 1; 0)
Phương trình tham số của đường thẳng d:
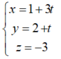
Chọn D.
Đáp án D
Mặt phẳng (P) có vecto pháp tuyến là: n p → (3; 1; 0)
Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: u d → = n p → (3; 1; 0)
Phương trình tham số của đường thẳng d:
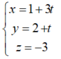
Chọn D.
Trong không gian oxyz phương trình đường thẳng d đi qua điểm M(3;0;-1) và có vecto chỉ phương a=(-1;2;3) là
A. \(\left\{{}\begin{matrix}x=3-t\\y=2t\\z=-1+3t\end{matrix}\right.\)
B. \(\left\{{}\begin{matrix}x=-1+3t\\y=2\\z=3-t\end{matrix}\right.\)
C. \(\left\{{}\begin{matrix}x=3+t\\y=2t\\z=-1-3t\end{matrix}\right.\)
D. \(\left\{{}\begin{matrix}x=-1-3t\\y=2\\z=3+t\end{matrix}\right.\)
Trong không gian Oxyz, cho 2 đường thẳng d : x = - 1 - 2 t y = t z = - 1 + 3 t , d ' : x = 2 + t ' y = - 1 + 2 t ' z = - 2 t ' và mặt phẳng (P): x + y + z + 2 = 0. Đường thẳng vuông góc với mặt phẳng (P), cắt d và d' có phương trình là
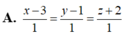
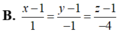
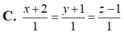
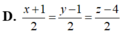
Trong không gian Oxyz, cho 2 đường thẳng d : x = - 1 - 2 t y = t z = - 1 + 3 t , d ' : x = 2 + t y = - 1 + 2 t z = - 2 t và mặt phẳng (P): x + y + z + 2 = 0. Đường thẳng vuông góc với mặt phẳng (P), cắt d và d' có phương trình là
A. x - 3 1 = y - 1 1 = z + 2 1
B. x - 1 1 = y - 1 1 = z - 1 - 4
C. x + 2 1 = y + 1 1 = z - 1 1
D. x + 2 2 = y - 1 2 = z - 4 2
Trong không gian OxyzOxyz cho hai điểm A(2;4;3)A(2;4;3) và B(2;7;1)B(2;7;1). Trong các phương trình dưới đây, phương trình nào là phương trình tham số của đường thẳng ABAB? (với t\in \Rt∈R)
A,\left\{{}\begin{matrix}x=2+2t\\y=7+4t\\z=1+3t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=7+4tz=1+3t
B,\left\{{}\begin{matrix}x=4\\y=3+3t\\z=2-2t\end{matrix}\right.⎩⎪⎨⎪⎧x=4y=3+3tz=2−2t
c,\left\{{}\begin{matrix}x=2\\y=4-3t\\z=3+2t\end{matrix}\right.⎩⎪⎨⎪⎧x=2y=4−3tz=3+2t
d,\left\{{}\begin{matrix}x=2+2t\\y=4+7t\\z=3+t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=4+7tz=3+t
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình lần lượt d: x = 1+2t, y = 2 - t, z = 3t . Tìm tọa độ điểm K đối xứng với điểm I(2;-1;3) qua đường thẳng d
A. K(4;3;3)
B. K(1;-3;3)
C. K(-4;-3;-3)
D. K(-1;3;-3)
Trong không gian oxyz, cho hai đường thẳng d1:\(\left\{{}\begin{matrix}x=-1+3t\\y=-t\\z=1-2t\end{matrix}\right.\)và d2:\(\dfrac{x-1}{-3}=\dfrac{y-2}{1}=\dfrac{z-3}{3}\)Vị trí tương đối của d1 và d2 là
A. song song
B. trùng nhau
C. cắt nhau
D. chéo nhau
Trong không gian Oxyz cho các đường thẳng d 1 : x + 2 y - 3 z + 1 = 0 2 x - 3 y + z + 1 = 0 và d 2 : x = 2 + a t y = - 1 + 2 t z = 3 - 3 t
Trong đó t là tham số, a là một số thực cho trước. Xác định a để tồn tại mặt phẳng (Q) chứa d 1 và vuông góc với d 2
A. a = -2
B. a = 2
C. a = -1
D. a = 1
Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A(1;-1;2), song song với mặt phẳng (P): 2x-y-z+3=0, đồng thời tạo với đường thẳng △ : x + 1 1 = y - 1 - 2 = z 2 một góc lớn nhất. Phương trình đường thẳng d là
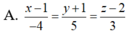
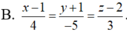
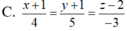
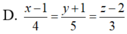
Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A(1;-1;2), song song với mặt phẳng (P): 2x-y-z+3=0, đồng thời tạo với đường thẳng ∆ : x + 1 1 = y - 1 - 2 = z 2 một góc lớn nhất. Phương trình đường thẳng d là.
![]()
![]()
![]()
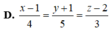
Tìm số giao điểm của mặt phẳng (α): x + y + z - 3 = 0 với đường thẳng d trong các trường hợp sau:
a ) d : x = 2 + t y = 3 - t z = 1 b ) d : x = 1 + 2 t y = 1 - t z = 1 - t c ) x = 1 + 5 t y = 1 - 4 t z = 1 + 3 t