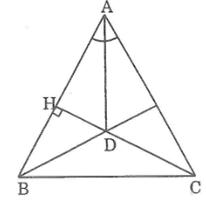
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.

Suy ra: AD ⊥ BC

Ta có: CH ⊥ AB (gt)

Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC

Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.

Vậy BD ⊥ AC.

mn giup mik vs

Bạn tự vẽ hình ik nha

a. Xét tam giác ABD và tam giác ACE có:

góc D = góc E = 90* (gt)

AB = AC (gt)

góc A chung

=> tg ABD = tg ACE (c. huyền-g. nhọn)

b. Vì H là giao điểm của 2 dường cao BD và CE 

Nên AH cũng là đường cao cùa tg ABC hay AH vuông góc BC

Do tg ABC là tam giác cân => AI là đường cao đồng thời cũng là dường trung tuyến => BI = CI => I là trung điểm của BC

c.Ta có: góc ACE = góc ABD (doc tg ABD = tg ACE)

 và góc ABC = góc ACB

=> góc DBC = góc ECB

 Ta có: BD vuông góc AC (gt)

              CF vuông góc AC (gt)

=>          CF song song BD (2 dường thẳng cùng vuông góc với 1 dường thẳng)

=>      góc DBC = góc BCF ( so le trong)

Mà góc DBC = góc ECB

=> góc ECB = góc BCF

=> BC lá tia phân giác của góc ECF

BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E

a) chứng minh AB=EB

b) chứng minh tam giác BED vuông

c) DE cắt AB tại F, chứng minh AE//FC

BÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại I

a) chứng minh tam giác IBC cân

b)lấy O thuộc tia IC sao cho IO=IE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quy

BÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB=15cm, BC=18cm

a)so sánh góc A và góc C

b)chứng minh rằng tam giác ABH = tam giác ACH

c)vẽ trung tuyến BD của tam giác ABC cắt AH tại G.Chứng minh rằng: tam giác AEG = tam giác ADG

d)tính độ dài AG

e) kẻ đường thẳng CG cắt AB ở E, chứng minh rằng: tam giác AEG = tam giác ADG

BÀI 4 cho tam giác ABC vuông tại A, trên BC lấy điểm D sao cho BA=BD.Qua D kẻ đường vuông góc với BC cắt AC tại E, qua C kẻ đường vuông góc với BE tại H cắt AB tại F

a)chứng minh tam giác ABE = tam giác DBE

b) chứng minh tam giác BCF cân

c) chứng minh 3 điểm F.D,E thẳng hàng

d)trên cạnh CB lấy điểm M sao cho CA=CM.Tính số đo góc DAM

BÀI 5 cho tam giác ABC cân tại A, kẻ BD vuông góc AC, kẻ CE vuông góc AB, BD và CE cắt nhau tại I

a)chứng minh rằng tam giác BDC = tam giác CEB

b)so sánh góc IBE và góc ICD

c) đường thẳng AI cắt BC tại H, chứng minh AI vuông góc BC tại H

BÀI 6 cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm

a)tính BC

b)trung trực của BC cắt AC tại D và cắt AB tại F, chứng minh góc DBC=DCB

c) trên tia đối của tia DB lấy E sao cho DE=DC, chứng minh tam giác BCE vuông và DF là phân giác góc ADE

d) chứng minh BE vuông góc FC

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
 => BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE. 
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
 =>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
 (Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của  ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE      => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực  Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/

(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
 => ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM          => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của  ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

a: AN=AB/2

AM=AC/2

mà AB=AC

nên AN=AM

=>ΔANM cân tại A

b: Xét ΔNBE vuông tại N và ΔMCD vuông tại M có

NB=MC

góc B=góc C

=>ΔNBE=ΔMCD

c: ΔNBE=ΔMCD

=>BE=CD

=>BD+DE=CE+DE

=>BD=CE

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

BD=CE

góc ABD=góc ACE

=>ΔADB=ΔAEC

=>AB=AC

=>ΔABC cân tại A

b: ΔABC cân tại A

mà AD là đường phân giác

nên AD vuông góc BC

Xét ΔABC có

AD,CH là đường cao

AD cắt CH tại D

=>D là trực tâm

=>BD vuông góc AC