Cho △PQR=△DEF trong đó PQ=5cm,QR=4cm,PR=3cm.
Chu vi tam giác DEF là:
Chu vi của tam giác PRQ là:
5+4+3=12(cm)
Mà theo đề bài thì tam giác PRQ=tam giác DEF
=>chu vi của tam giác DEF là 12cm
Cho ∆ PQR = ∆DEF trong đó PQ = 8cm, QR = 5cm, PR= 9cm. Chu vi tam giác DEF là
Cho biết \(\Delta{MNP}=\Delta{DEF}\) và MN = 4cm, MP = 5cm, EF = 6cm. Tính chu vi tam giác MNP.
Vì \(\Delta{MNP}=\Delta{DEF}\)
\( \Rightarrow DE = MN;EF = NP;DF = MP\) (các cạnh tương ứng)
\( \Rightarrow NP = 6cm\)
\( \Rightarrow \) Chu vi tam giác MNP là:
C = MN + MP + NP = 4 + 5 + 6 = 15 (cm)
Đúng 0
Bình luận (0)
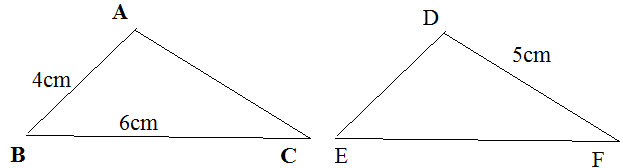
Cho \(\Delta ABC=\Delta DEF\). Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó) ?
Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)
Đúng 0
Bình luận (0)
Ta có \(\Delta\)ABC= \(\Delta\)DEF
Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.
Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)
Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm )
Đúng 0
Bình luận (0)
vì tam giác ABC = tam giác DEF
Nên AB = DE= 4cm
BC= EF = 6 cm
AC= DF = 5 cm
lúc đó:chu vi tam giác ABC= tam giác DEF= 4+5+6=15(cm)
Vậy chu vi tam giác ABC = chu vi tam giác DEF=15cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27cm. Biết rằng AB=4cm, BC=6cm, DE=6cm, FD=12cm. Chứng minh ΔABC ∽ ΔDEF
Vì chu vi tam giác ABC bằng 18cm
=> AB+AC+BC=18 => 4+AC+6=18 => AC=8 (cm)
Vì chu vi tam giác DEF bằng 27cm
=> DE+EF+DF=27 => 6+EF+12=27 => EF=9 (cm)
Ta thấy \(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\\ = \frac{4}{6} = \frac{8}{{12}} = \frac{6}{9} = \frac{2}{3}\end{array}\)
=> ΔABC ∽ ΔDEF
Đúng 1
Bình luận (0)
Cho ΔABC = ΔDEF. Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi mỗi tam giác là tổng độ dài ba cạnh của tam giác đó).
Hình vẽ
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Vậy...
Chúc bạn học tốt!
\(Cho\Delta ABC\) và \(\Delta DEF\) biết \(\widehat{B}=\widehat{F}\) và AB = EF
a) Với điều kiện nào thì 2 tam giác trên bằng nhau trong trường hợp ( c.g.c), viết kí hiệu về sự bằng nhau của 2 tam giác đó
b) Cho 2 tam giác ABC va DEF bằng nhau như câu a. TÍnh chu vi mỗi tam giác nói trên, biết AB = 5cm , AC = 6cm, DF = 6cm ?
a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác AMN bằng tam giác PQR biết AM bằng 6cm, AN bằng 4cm và QR bằng 5cm. Tính chu vi của mỗi tam giác
Do \(\Delta AMN=\Delta PQR\)=> PQ = AM = 6cm , PR = AN = 4cm , MN = QR = 5cm .
Chu vi \(\Delta AMN\)bằng chu vi \(\Delta PQR\)và bằng là : 6 + 4 + 5 = 15cm.
Đúng 0
Bình luận (0)
Cho tam giác MNP=tam giácDEF, biết MN=3cm,MP=5cm,EF=6cm. Chu vi của tam giác DEF là
A.10cm
B12cm
C.14cm
D.16cm
Xem thêm câu trả lời
Tìm tam giác vuông trong các tam giác sau:
a) Tam giác \(EFK\) có \(EF = 9\)m, \(FK = 12\)m, \(EK = 15\)m.
b) Tam giác \(PQR\) có \(PQ = 17\)cm, \(QR = 12\)cm, \(PR = 10\)cm.
c) Tam giác \(DEF\) có \(DE = 8\)m, \(DF = 6\)m, \(EF = 10\)m.
a: EK^2=EF^2+FK^2
=>ΔEFK vuông tại F
b: PQ^2<>QR^2+PR^2
=>ΔPRQ ko vuông
c: EF^2=DE^2+DF^2
=>ΔDEF vuông tại D
Đúng 0
Bình luận (0)