Trên trục số cho 2 điểm a , b .Hãy:
a, Xác định các điểm -a , -b trên trục số;
b, Xác định các điểm I a I, I b I , I -a I , I -b I trên trục số ;
c, So sánh các số a, b, -a, -b, I a I , I b I , I -a I , I -b I với 0.
Trên trục số cho hai điểm a, b. Hãy:
a) Xác định các điểm –a, -b trên trục số;
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số;
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0.

a) Xác định các điểm –a, -b trên trục số:

b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:

c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số ⇒ a là số nguyên âm nên a < 0.
Do đó: -a = |-a| = |a| > 0.
b ở bên phải trục số ⇒ b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
Trên trục số cho 2 điểm a,b(h.53).Hãy:
a)Xác định các điểm -a,-b trên trục số;
b)Xác định các điểm |a|,|b|,|-a|,|-b| trên trục số;
c)So sánh các số a,b,-a,-b,|a|,|b|,|-a|,|-b| với 0.
Trên trục số cho 2 điểm a,b(h.53).Hãy:
a)Xác định các điểm -a,-b trên trục số;
b)Xác định các điểm |a|,|b|,|-a|,|-b| trên trục số;
c)So sánh các số a,b,-a,-b,|a|,|b|,|-a|,|-b| với 0.
Trên trục số cho hai điểm a, b. Hay :
a, Xác định các điểm -a,-b trên trục số;
b, Xác định các điểm |a|,|b|,|-a|,|-b| trên trục số;
c, So sánh các số a,b,-a,-b,|a|,|b|,|-a|,|-b| voi 0.
trên trục số có hai điểm a , b (h.53).hãy a, xác định các điểm -a , -b trên trục số b, xác định các điểm / a/ , / b/ , /-a/,/-b/ trên trục số ; c, so sánh các số a,b,-a,-b,/a/,/b/,/-a/,/-b/ với 0
ai học lớp 6 thì giở trang 89 sgk toán có cần làm không hay là xác định thôi
đề bài là:
trên trục số cho 2 điểm a,b. Hãy:
a, Xác định các điểm -a,-b trên trục số
b, Xác định các điểm |a|,|b|,|-a|,|-b| trên trục số.
c, So sánh a,b,-a,-b,|a|,|b|,|-a|,|-b| với 0
Trên trục số cho hai điểm a, b (h.53). Hãy :
a) Xác định các điểm : \(-a,-b\) trên trục số
b) Xác định các điểm \(\left|a\right|,\left|b\right|,\left|-a\right|,\left|-b\right|\) trên trục số :
c) So sánh các số \(a,b,-a,-b,\left|a\right|,\left|b\right|,\left|-a\right|,\left|-b\right|\) với 0
a) Xác định các điểm –a, -b trên trục số:
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số => a là số nguyên âm nên a < 0.
Do đó: -a = |a| = |a| > 0.
b ở bên phải trục số => b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
Bài giải:
a) Xác định các điểm –a, -b trên trục số:
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số => a là số nguyên âm nên a < 0.
Do đó: -a = |a| = |a| > 0.
b ở bên phải trục số => b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
Trên trục số cho hai điểm c, d (hình dưới)

Xác định các điểm –c, -d trên trục số
Xác định các điểm |c|, |d|, |-c|, |-d| trên trục số
Cac điểm –c, -d, |c|, |d| |-c|, |-d| được biểu diễn trên trục số:

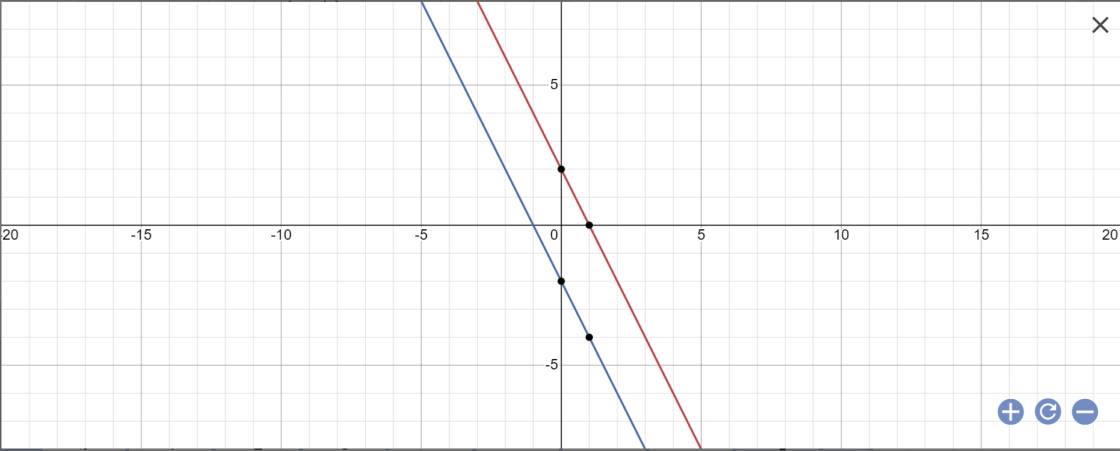
Cho hàm số: y=-2x+2 có đồ thị là d1.
a) Xác định tọa độ các điểm A và B lần lượt là giao điểm của d1 với các trục Ox,Oy của hệ trục tọa độ Oxy (đơn vị trên các trục được tính là cm).
b) Viết phương trình đường thẳng d2 cắt các Ox,Oy lần lượt tại C và D sao cho tứ giác ABCD là hình thoi.
c) Vẽ d1 và d2 và tính diện tích của hình thoi ABCD.
a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2