Cho phương trình
x^2-3x+1
Có hai nghiệm là x1;x2
Đặt An=x1n;x2n(n>0)
a)CMR An+2=3Aa+1 - An
b)CMR An là số nguyên
c)CMR An-2 = [((căn5 + 1)/2)^n - ((căn5 - 1)/2)^n)]^2
d) Tìm n để An-2 Là số chính phương
Cho phương trình 2 - 3 x + 2 + 3 x = 4 . Gọi x 1 , x 2 x 1 < x 2 là hai nghiệm thực của phương trình. Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Tìm m để hệ phương trình:
{3x - y = 2m + 3
{x + 2y = 3m + 1
có nghiệm (x;y) thỏa mãn x^2 + y^2 = 5
\(HPT\Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m+6\\x+2y=3m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=7m+7\\x+2y=3m+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=m+1\\m+1+2y=3m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+1\\y=m\end{matrix}\right.\)
\(x^2+y^2=5\Leftrightarrow m^2+2m+1+m^2=5\\ \Leftrightarrow2m^2+2m-4=0\\ \Leftrightarrow m^2+m-2=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Cho x1, x2 là hai nghiệm của phương trình x 2 - 3 x + 2 = 0 .Trong các phương trình sau đây, phương trình nào chỉ có hai nghiệm là x 1 x 2 + 1 v à x 2 x 1 + 1 .
![]()
![]()
![]()
![]()
Đáp án: A
![]()
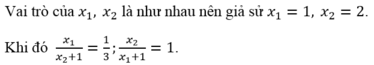
Ta tìm phương trình có 2 nghiệm là ![]() và 1. Ta có thể thử nghiệm vào từng phương trình xem phương trình nào thỏa mãn hoặc giải từng phương trình rồi so sánh nghiệm.
và 1. Ta có thể thử nghiệm vào từng phương trình xem phương trình nào thỏa mãn hoặc giải từng phương trình rồi so sánh nghiệm.

⇒ Chọn đáp án A.
1.Rút gọn biểu thức: P= √x/√x+1 + 2√x/x +1 - 3x+1/x-1 (với x>= 0 , x khác 1)
2.Cho Phương trình x^2mx-1=0 (m là Tham số)
a)Chứng minh luôn có hai nghiệm phân biệt
b)Tìm m để phương trình có hai nghiệm x1,x2 thỏa mãn x1^2+x2^2=7
1, Với x >= 0 ; x khác 1
\(P=\dfrac{\sqrt{x}\left(x-1\right)+2\sqrt{x}\left(\sqrt{x}-1\right)-\left(3x+1\right)\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x\sqrt{x}+2x-3\sqrt{x}-3x\sqrt{x}-3x-\sqrt{x}-1}{\left(x-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2x\sqrt{x}-x-4\sqrt{x}-1}{\left(x-1\right)\left(\sqrt{x}+1\right)}\)
mình sửa đề câu 2 nhé
a, \(x^2+mx-1=0\)
\(\Delta=m^2-4\left(-1\right)=m^2+4>0\)
Vậy pt luôn có 2 nghiệm pb
b, Theo Vi et : \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=-1\end{matrix}\right.\)
Ta có : \(\left(x_1+x_2\right)^2-2x_1x_2=7\)
Thay vào ta được : \(m^2+2=7\Leftrightarrow m^2=5\Leftrightarrow m=\pm\sqrt{5}\)
2.a) Để phương trình luôn có 2 nghiệm phân biệt thì: `Delta>0`
Delta=\(\left(-2m\right)^2\)-4.1.(-1)
<=>\(4m^2\)+4>0(∀m∈R)
Vậy phương trình luôn có 2 nghiệm phân biệt (∀m)
b. theo hệ thức viet, ta có:
x1+x2=2m
x1.x2=-1
\(x1^2+x2^2-x1x2=7\)
\(\Leftrightarrow\left(x1+x2\right)^2-3.x1.x2=7\)
\(\Leftrightarrow\left(2m\right)^2-3.\left(-1\right)=7\)
\(\Leftrightarrow4m^2=4\)
\(\Leftrightarrow m^2=1\)
=> m=1 , m= -1
Cho phương trình
2 - 3 x + 2 + 3 x = 4 . Gọi x 1 , x 2 x 1 < x 2 là hai nghiệm thực của phương trình. Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Cho phương trình 3 . 25 x - 2 + ( 3 x - 10 ) . 5 x - 2 + 3 - x = 0 Phương trình trên có hai nghiệm x1,x2 với x1<x2 Giá trị P=x2-x1 bằng bao nhiêu?
A. P = log 5 3
B. P = 2 - log 5 3
C. P = 4 - log 5 3
D. P = - log 5 3
Cho phương trình: x2 - 5x +m -1 = 0 (m là tham số). a) Giải phương trình trên khi m = -5. b) Tìm m để phương trình trên có hai nghiệm x1, X2 thỏa mãn: x1-x= 3. c) Tìm m để phưrơng trình trên có hai nghiệm x1, X2 thỏa mãn 2x, - 3x, = 5 d) Tìm m để phương trình trên có hai nghiệm x1, X2 thòa mãn (x - 1) +(x, -1) = 5 e) Tìm m đề phương trình trên có hai nghiệm x1, X2 thỏa mãn (x, - 1) +(x,-1) +2x,x, <5 g) Tìm m để phương trình trên có hai nghiệm x1, X2 thỏa mãn x <1
a: Khi m=-5 thì pt sẽ là x^2-5x-6=0
=>x=6 hoặc x=-1
b:
Δ=(-5)^2-4(m-1)=25-4m+4=-4m+29
Để pt có hai nghiệm thì -4m+29>=0
=>m<=29/4
x1-x2=3
=>(x1-x2)^2=9
=>(x1+x2)^2-4x1x2=9
=>5^2-4(m-1)=9
=>4(m-1)=25-9=16
=>m-1=4
=>m=5(nhận)
c: 2x1-3x2=5 và x1+x2=5
=>x1=4 và x2=1
x1*x2=m-1
=>m-1=4
=>m=5(nhận)
cho pt x^2 -3x +m-2 =0 gọi x1,x2 là hai nghiệm của phương trình .Tìm giá trị của m để x1^3 -x2^3 +9x1x2=81
Để pt: \(x^2-3x+m-2=0\) có hai nghiệm : \(x_1;x_2\) điều kiện là:
\(\Delta=9-4\left(m-2\right)\ge0\)
<=> \(m\le\frac{17}{4}\)( @@)
Áp dụng định lí viet ta có:
\(\hept{\begin{cases}x_1+x_2=3\\x_1.x_2=m-2\end{cases}}\)=> \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=9-4\left(m-2\right)=17-4m\ge0\)
=> \(x_1-x_2=\sqrt{17-4m}\)
Ta có:
\(x_1^3-x_2^3+9x_1x_2=\left(x_1-x_2\right)^3+3\left(x_1-x_2\right)x_1x_2+9x_1x_2\)
\(=\sqrt{\left(17-4m\right)^3}+3\sqrt{17-4m}\left(m-2\right)+9\left(m-2\right)\)
Theo bài ra ta có phương trình:
\(\sqrt{\left(17-4m\right)^3}+3\sqrt{17-4m}\left(m-2\right)+9\left(m-2\right)=81\)
<=> \(\left(\sqrt{17-4m}\right)^3-3^3+3\left(m-2\right)\left(\sqrt{17-4m}-3\right)=0\)
<=> \(\left(\sqrt{17-4m}-3\right)\left(17-4m+3\sqrt{17-4m}+9+3\left(m-2\right)\right)=0\)
<=> \(\left(\sqrt{17-4m}-3\right)\left(20-m+3\sqrt{17-4m}\right)=0\)
TH1: \(\sqrt{17-4m}-3=0\Leftrightarrow17-4m=9\Leftrightarrow m=2\left(tm@@\right)\)
TH2: \(20-m+3\sqrt{17-4m}=0\)
<=> \(3\sqrt{17-4m}=m-20\)=> \(m-20\ge0\)=> \(m\ge20\) vô lí với (@@)
Vậy m = 2.
Cho x1, x2 là hai nghiệm của phương trình: x^2-2x-1=0.Hãy lập một phương trình bậc hai một ẩn có hại nghiệm là x1+(x2)^2 và x2+(x1)^2
\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)
Cho phương trình: x2 + 3x + m – 1 = 0 (x là ẩn số).
a) Giải phương trình khi m = 3
b) Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn: x1(x14 – 1) + x2(32x24 –1) = 3