Câu 12: Cho tam giác ABC có góc A bằng 450 ; góc B bằng 750. Ta có:
A. AB< BC < CA B. BC < AB < AC
C. CA < AB < BC D. CA < BC< AB
Câu 1 : Cho tam giác ABC có B - C = 30 độ . Tia phân giác của góc A cắt cạnh BC ở D. Tính góc ADB .
A. 300 B. 450 C. 600 D. 750
Câu 2 : Cho tam giác ABC ; A = 500 ; B : C = 2 : 3. Số đo các góc B và C lần lượt là:
A. 480 ; 820 B. 540 ; 760
C. 520 ; 780 D. 320 ; 880
CÁC BẠN GIẢI THÍCH CÁC BƯỚC SAO RA ĐƯƠC KẾT QUẢ GIÚP MIK VỚI NHA.
MIK CẢM ƠN NHIỀU NHA ^^
Câu 56: Nếu \(\sqrt{-x=6}\) thì x có giá trị là : A.-36 B.36. C.12 D.-12
Câu 57: Cho\(\Delta\)ABC có A=450 biết B=2C tam giác ABC là tam giác gì:
A.Tam giác nhọn B. Tam giác tù C. Tam giác vuông Câu 62: Giá trị của x trong phép tính:\(-x.\dfrac{11}{2}+\dfrac{5}{4}=-1,5\) là:
A. 2 B. 0,5 C. -2 D. -0,5
Câu 63: Cho x và y là hai đại lượng tỉ lệ thuận và khi x = 6 thì y = 4. Hệ số tỉ lệ k của y đối với x là: A. k = 24 B. k = \(\dfrac{2}{3}\) C. k =\(\dfrac{3}{2}\) D. k = \(\dfrac{1}{24}\)
Câu 64: Hai số x và y thỏa món điều kiện \(\dfrac{x}{3}=\dfrac{y}{5}\) và x + y = -16 là:
A. x = 48; y = 90 B. x = 6; y = 10 C. x = 24; y = 40 D. x = -6; y = -10
Câu 67: Chọn khẳng định đúng
A. Có duy nhất một đường thẳng song song với đường thẳng cho trước.
B. Nếu ba góc của tam giác này bằng ba góc của tam giác kia thì hai tam giac đó bằng nhau.
C. Góc ngoài của tam giác lớn hơn mỗi góc trong của tam giác.
D. Mỗi đoạn thẳng chỉ có một trung trực.
Chọn câu đúng nhất.1 .Cho ∆ ABC vuông cân tại A. vậy góc B bằng:A. 600B. 900C. 450D. 12002. Một tam giác là vuông nếu độ dài 3 cạnh của nó là:A. 2,3,4 B. 3,4,5 C. 4,5,6 D. 6,7,83. Một tam giác cân có góc ở đáy là 350 thì góc ở đỉnh có số đo là:A. 1000B. 1100C. 850D. 12004. Tam giác ABC có BC = 3cm ; AC = 5cm ; AB = 4cm. Tam giác ABC vuông tại đâu?A. Tại B B. Tại C C. Tại A D. Không phải là tam giác vuông5. Tam giác ABC có AB = AC = BC thì tam giác ABC là A. Tam giác nhọn B. Tam giác cân C. Tam giác vuông D. Tam giác đều6. Tam giác nào vuông nếu độ lớn ba góc kà:A. 300, 700, 800B. 200, 700, 900 C. 650, 450, 700D. 600, 600, 6007. Tam giác cân là tam giác có:A. Hai cạnh bằng nhau -B. Ba cạnh bằng nhau - C. Một góc bằng 600 - D. Một góc bằng 900
Câu 1: Tam giác DEF vuông tại D có tổng hai góc nhọn E và F bằng : ......
Câu 2: Cho tam giác ABC có AB=AC , M là trung điểm của BC thì ta có 2 tam giác bằng nhau là : .....
Câu 3: Cho tam giác ABC và tam giác MNP có AB =MN , góc A = góc M . Để tam giác ABC = tam giác MNP thao trường hợp (c.g.c) thì cần thêm điều kiện là:....
câu 1 E + F = 90 độ
câu 2 góc AMB và góc AMC
câu 3 AC = MP
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
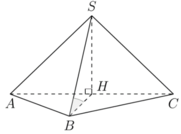
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho lăng trụ ABCA’B’C’ có đáy ABC là tam giác đều cạnh 2 α . Hình chiếu vuông góc của A’ trên (ABC) là trung điểm H của BC, góc giữa AA’ và (ABC) bằng 450. Thể tích của khối lăng trụ ABCA’B’C’ bằng
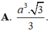
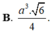
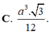
![]()
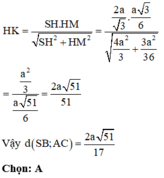
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a và ∠ S B A = ∠ S C A = 90 0 . Biết góc giữa đường thẳng SA và mặt phẳng ABC bằng 45 0 . Khoảng cách giữa hai đường thẳng SB và AC là:
A. 2 51 17 a
B. 2 7 7 a
C. 39 13 a
D. 2 13 13 a

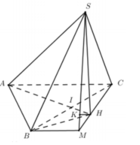



Áp dụng hệ thức lượng trong tam giác vuông SMH ta có:
Cho tam giác ABC Có góc A=1050; góc B=450; BC=4cm. Tính AB, AC
\(\dfrac{a}{SinA}=\dfrac{b}{SinB}=\dfrac{c}{SinC}\)
\(\Rightarrow\dfrac{4}{Sin105}=\dfrac{AC}{Sin45}=\dfrac{AB}{Sin30}=4\sqrt{6}-4\sqrt{2}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=2\sqrt{6}-2\sqrt{2}\\AC=-4+4\sqrt{3}\end{matrix}\right.\) ( cm )
Vậy ..
Vẽ đường cao AH
Ta có: ΔAHB vuông tại H(gt)
mà \(\widehat{B}=45^0\)
nên ΔAHB vuông cân tại H
⇔\(BH=AH=HC\cdot\tan30^0\)
\(\Leftrightarrow BH-CH\cdot\tan30^0=\dfrac{CH}{\sqrt{3}}\)
\(\Leftrightarrow BH=\dfrac{4}{1+\sqrt{3}}\)
\(\Leftrightarrow AB=\dfrac{AH}{\sin45^0}\simeq2,06\left(cm\right)\)
\(\Leftrightarrow AC=2\cdot AH=2,92\left(cm\right)\)