Tam giác ABC, B(1;2) phân giác trong của góc A có pt là 2x+y-1=0, khoảng cách từ C đến phân giác đó gấp 3 lần khoảng cách từ B đến phân giác đó, C thuộc trục tung. Tìm các đỉnh còn lại của tam giác

Những câu hỏi liên quan
Câu 1:
1) Cho tam giác ABC có góc A = góc C-10độ; góc B=góc C + 10độ. Tính các góc của tam giác ABC?
2) Cho tam giác ABC có góc B= 7/6 góc C; góc A= 5/6 góc C. Tính các góc của tam giác ABC?
3) cho tam giác ABC có góc A= 2. Góc B ; góc B = góc C . tính các góc của tam giác ABC?
4) Cho tam giác ABC có góc A= 5.góc C; góc B= 2.góc C. tínhcác góc của tam giác ABC?
Câu 1 :1, cho tam giác abc có ab=5cm , ac = 12cm , bc=13 cm
a. Tam giác abc là tam giác gì?
b. so sánh các góc của tam giác abc
Bài 1:
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: Vì AB<AC<BC
nên góc C<góc B<góc A
Đúng 0
Bình luận (0)
cho tam giác ABC với A<3,1> ,B<-1,-1> , C <6,0>
a, tính AB*AC
b, tính diện tích tam giác ABC
c, tìm tọa độ trực tâm H của tam giác ABC
d, tìm tọa độ trọng tâm G của tam giác ABC
e, tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC từ đó chứng minh rằng I,H,G thẳng hàng
Trong mặt phẳng tọa độ Oxy
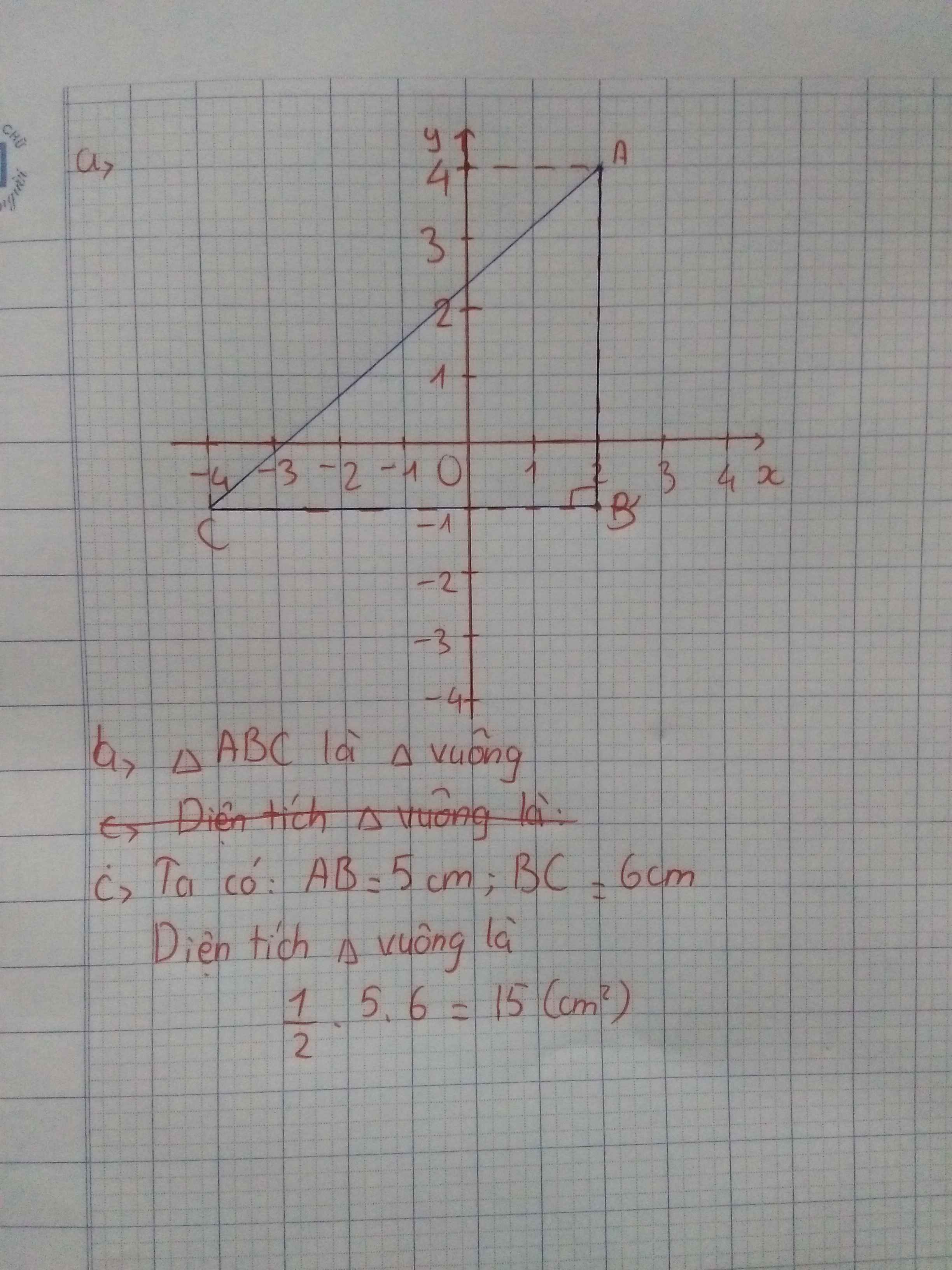
a) Vẽ tam giác ABC, biết A(2;4) ; B(2;-1) ; C(-4;-1)
b) Tam giác ABC là tam giác gì ? Tính diện tích của tam giác đó.
b) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(2-2\right)^2+\left(4+1\right)^2}=5\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(2+4\right)^2+\left(4+1\right)^2}=\sqrt{61}\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(2+4\right)^2+\left(-1+1\right)^2}=6\)
Ta có: \(BA^2+BC^2=5^2+6^2=25+36=61\)
\(AC^2=\left(\sqrt{61}\right)^2=61\)
Do đó: \(AC^2=BA^2+BC^2\)(=61)
Xét ΔABC có \(AC^2=BA^2+BC^2\)(cmt)
nên ΔABC vuông tại B(Định lí Pytago đảo)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{BA\cdot BC}{2}=\dfrac{5\cdot6}{2}=\dfrac{30}{2}=15\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có độ dài như sau: A(1;1), B(5;1), C(7;9)
a) Tính A, B, C của tam giác ABC
b) Gọi AA1, BB1, CC1 là các đường phân giác trong của tam giác ABC. Tính tỷ số diện tích của tam giác A1B1C1 và tam giác ABC
Trong mp xOy cho tam giác ABC. bt A(3;-1) B(-1;2) I(1;-1) là trọng tâm của tam giác ABC. Trực tâm H của tam giác ABC có tọa độ (a;b). Tính a+3b
Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
câu 1: Cho tam giác ABC có B=C=45 độ.khi đó tam giác ABC là tam giác gì
Lời giải:
$\widehat{A}+\widehat{B}+\widehat{C}=180^0$
$\Rightarrow \widehat{A}=180^0-\widehat{B}-\widehat{C}=180^0-45^0-45^0=90^0$
$\Rightarrow$ tam giác $ABC$ là tam giác vuông tại $A$. Mà $\widehat{B}=\widehat{C}$ nên $ABC$ là tam giác vuông cân ở A
Đúng 2
Bình luận (0)
cho tam giác ABC có A<5,3> B<-2,-1> C<-1,5 >
a, tính <AB +2BC>*AC , < AB-2BC> *BC
b, tìm tọa độ trọng tâm tam giác ABC
c, tìm tọa độ trực tâm tâm của tam giác ABC
d, tim tọa độ chân đường cao A của tam giác ABC
e, tính diện tích tam giác ABC
cho tam giác ABC có A<5,3> B<-2,-1> C<-1,5 >
a, tính <AB +2BC>*AC , < AB-2BC> *BC
b, tìm tọa độ trọng tâm tam giác ABC
c, tìm tọa độ trực tâm tâm của tam giác ABC
d, tim tọa độ chân đường cao A của tam giác ABC
e, tính diện tích tam giác ABC
Cho tam giác ABC cân tại A có AB=AC=b ; BC=a. Phân giác BD của tam giác ABC có độ dài bằng cạnh bên
của tam giác ABC. Chứng minh rằng: 1/b-1/a=b/(a+b)^2