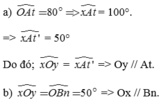cho xOy =50. trên tia đối của tia Ox lấy điểm A. vẽ tia Am là tia đối của tia Ax. trên nửa mặt phẳng bờ mx chứa xOy vẽ ti At mà mAt =130. chứng minh at song song oy.chứng minh tia phân giác của OAt và xOy song song với nhau

Những câu hỏi liên quan
cho xOy =50. trên tia đối của tia Ox lấy điểm A. vẽ tia Am là tia đối của tia Ax. trên nửa mặt phẳng bờ mx chứa xOy vẽ ti At mà mAt =130. chứng minh at song song oy. chứng minh tia phân giác của OAt và xOy song song với nhau
Mình đang bận làm đề tiếng anh nên tý nữa mình sẽ giúp bạn. Không liên quan nhưng mà cũng fan TaeYeon này. Hit mới ra "WHY" với "STARLIGHT" hay dã man =))
Đúng 0
Bình luận (1)
Bây h mình khg có thước đo góc chứ có mình sẽ giúp bạn
Đúng 0
Bình luận (0)
ôi fan taeyeon hả. mik là fan cứng nè. công nhận why với starlight hay quá trời
Đúng 0
Bình luận (0)
Cho
x
O
y
^
120°. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho
O
A
t
^
60°. Gọi At là tia đối của tia At.a) Chứng minh tt // Oy.b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An
Đọc tiếp
Cho x O y ^ = 120°. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60°. Gọi At' là tia đối của tia At.
a) Chứng minh tt' // Oy.
b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An
a) O A t ^ + x O y ^ = 60°+ 120° = 180° (hai góc trong cùng phía bù nhau)
=> At // Oy => tt' // Oy
b) Vì Om là phân giác x O y ^ nên:
x O m ^ = 1 2 x O y ^ = 1 2 .120° = 60° (1)
Mặt khác : O A t ^ = 60 ° = > x A t ^ = 120°
Vì An là phân giác x A t ^ nên:
x A n ^ = 1 2 x A t ^ = 1 2 .120° = 60° (2)
Từ (1) và (2) suy ra x O m ^ = x A n ^ .
Do đó Om // An
Đúng 0
Bình luận (0)
Cho
x
O
y
^
50
°
. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy, vẽ tia At sao cho At cắt Oy tại B và
O
A
t
^
80
°
. Gọi At là tia phân giác của góc
x
A
t
^
.a) Chứng minh At // Oy.b)...
Đọc tiếp
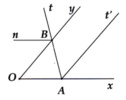
Cho x O y ^ = 50 ° . Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy, vẽ tia At sao cho At cắt Oy tại B và O A t ^ = 80 ° . Gọi At' là tia phân giác của góc x A t ^ .
a) Chứng minh At' // Oy.
b) Trên nửa mặt phẳng không chứa điểm A, bờ là đường thẳng Oy, vẽ tia Bn sao cho O B n ^ = 50 ° . Chúng minh Bn // Ox.
Cho góc xOy = 120°. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là tia Ox, vẽ tia At sao cho góc OAt = 60°. Gọi At' là tia đối của tia At. a) Chứng minh tt' // Oy. b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An
a: \(\widehat{tAO}+\widehat{xOy}=180^0\)
mà hai góc này trong cùng phía
nên tt'//Oy
b: \(\widehat{xAt}+\widehat{tAO}=180^0\)
=>\(\widehat{xAt}=180^0-60^0=120^0\)
=>\(\widehat{xAn}=\dfrac{120^0}{2}=60^0\)
Om là phân giác của góc xOy
=>\(\widehat{xOm}=\dfrac{1}{2}\cdot120^0=60^0\)
\(\widehat{xOm}=\widehat{xAn}\)
mà hai góc này ở vị trí đồng vị
nên Om//An
Đúng 0
Bình luận (0)
góc xOy120 độ , lấy điểm A trên tia Ox . trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho góc OAt60 độ . gọi At` là tia đối của tia Ata, chứng minh rằng : tt` // Oyb, gọi Om // An là phân giác của góc xOy và góc OAtchứng minh rằng : Om // An
Đọc tiếp
góc xOy=120 độ , lấy điểm A trên tia Ox . trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho góc OAt=60 độ . gọi At` là tia đối của tia At
a, chứng minh rằng : tt` // Oy
b, gọi Om // An là phân giác của góc xOy và góc OAt
chứng minh rằng : Om // An
Cho
x
O
y
^
120
°
. Lấy điêm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho
O
A
t
^
60
°
. Gọi At là tia đối của tia At.a) Chứng minh tt // Oy.b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An
Đọc tiếp
Cho x O y ^ = 120 ° . Lấy điêm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60 ° . Gọi At' là tia đối của tia At.
a) Chứng minh tt' // Oy.
b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An
Cho xOy=120 độ . Lấy điểm A trên tia Ox . Trên cùng nửa mặt phẳng chứa tia Oy bờ là Ox vẽ tia At sao cho OAt=60 độ . Gọi At' là tia đối của tia At
a/ Chứng minh tt'//Oy
b/ Gọi Om, An theo thứ tự là các tia phân giác của góc xOy; xAt; Chứng minh Om//An
a, Vì \(\widehat{xOy}+\widehat{OAt}=180^0\) mà 2 góc này ở vị trí trong cùng phía nên Oy//At
Mà tt' trùng At nên Oy//tt'
b, Vì Om là p/g xOy nên \(\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}\)
Vì An là p/g tAx nên \(\widehat{xAn}=\dfrac{1}{2}\widehat{tAx}=\dfrac{1}{2}\widehat{xOy}\left(đồng.vị\right)\)
Do đó \(\widehat{xOm}=\widehat{xAn}\) mà 2 góc này ở vị trí đồng vị nên Om//An
Đúng 2
Bình luận (0)
. Cho xOy =120 độ . Lấy điểm A trên tia Ox . Trên cùng một nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho OAt = 60 độ . Gọi At' là tia đối tia At . a) Chứng minh tt ' // Oy . b) Gọi Om và An theo thứ tự là các tia phân giác của góc xOy và xAt . Chứng minh Om // An
Cho xOy =50 độ. Lấy điểm A trên tia Ox . Trên cùng nửa mặt phẳng bờ Ox chứa Oy, vẽ tia At sao cho At cắt Oy tại B và OAt = 80 độ . Gọi At' là tia phân giác của góc xAt.
a, Chứng minh At' // Oy
b, Trên nửa mawtjj phẳng ko chứa điểm A , bờ là đường thẳng Oy, vẽ tia Bn sao cho OBn =50 độ . Chứng minh Bn// Ox
HELP ME!
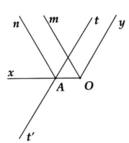
\(a)O\widehat{A}T=80^o\Rightarrow x\widehat{At}=100^{^{ }o}\)
\(\Rightarrow x\widehat{At}'=50^o\)
Do đó,\(x\widehat{O}y=x\widehat{At}'\Rightarrow OY//AT\)
B)\(x\widehat{Oy}=O\widehat{Bn}=50^o\Rightarrow OX//BN\)
Đúng 4
Bình luận (0)