a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có

\(\widehat{ACB}\) chung

Do đó: ΔABC đồng dạng với ΔHAC

b: Xét ΔKHB vuông tại K và ΔKAH vuông tại K có

\(\widehat{KHB}=\widehat{KAH}\left(=90^0-\widehat{B}\right)\)

Do đó: ΔKHB đồng dạng với ΔKAH

=>\(\dfrac{KH}{KA}=\dfrac{KB}{KH}\)

=>\(KH^2=KA\cdot KB\)

c: Ta có: ΔAHC vuông tại H

=>\(HC^2+HA^2=AC^2\)

=>\(HA^2=10^2-8^2=36\)

=>\(HA=\sqrt{36}=6\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(HB=\dfrac{6^2}{8}=4,5\left(cm\right)\)

BC=BH+CH

=4,5+8

=12,5(cm)

Xét ΔABC có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot12,5\cdot6=3\cdot12,5=37,5\left(cm^2\right)\)

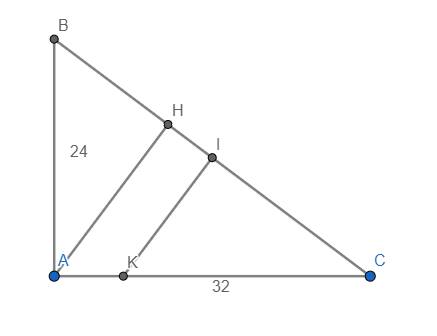
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\)) 

Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)

Nên \(\widehat{HAC}\approx53,13^o\)

Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm

\(\Rightarrow IB=IC=20cm\)

Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\) 

\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)

Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)

Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)

\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)

Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)

Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)

\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có

góc C chung

Do đó: ΔABC\(\sim\)ΔHAC

b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có

góc HBA=góc HAC

Do đó: ΔHBA\(\sim\)ΔHAC

Suy ra: HB/HA=HA/HC

hay \(HA^2=HB\cdot HC\)

a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:

\(\widehat{B}\) là góc chung, \(\widehat{AHB}=\widehat{BAC}=90^o\)

=> \(\Delta HBA~\Delta ABC\) (g.g) (1)

b) Xét \(\Delta HAC\) và \(\Delta ABC\) có:

\(\widehat{C}\) là góc chung, \(\widehat{AHC}=\widehat{BAC}=90^o\)

=> \(\Delta HAC~\Delta ABC\) (g.g) (2)

Từ (1) và (2) suy ra \(\Delta HBA~\Delta HAC\)

=> \(\frac{S_{\Delta HBA}}{S_{\Delta HAC}}=\left(\frac{AB}{AC}\right)^2=\left(\frac{12}{16}\right)^2=\left(\frac{3}{4}\right)^2=\frac{9}{16}\)

a) Xét tam giác ABC và tam giác HAC có :

\(\widehat{BAC}=\widehat{AHC}\left(=90^o\right)\)

Chung \(\widehat{ACB}\)

\(\Rightarrow\) tam giác ABC đồng dạng với tam giác HAC (g-g) (đpcm)

b) Xét tam giác ABC và tam giác HBA có :

\(\widehat{BAC}=\widehat{AHB}\left(=90^o\right)\)

Chung \(\widehat{ABC}\)

\(\Rightarrow\) tam giác ABC đồng dạng với tam giác HBA (g-g)

Mà tam giác ABC đồng dạng với tam giác HAC ( câu a )

Suy ra tam giác HBA đồng dạng với tam giác HAC

\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Leftrightarrow HA^2=HB\times HC\left(đpcm\right)\)

c) Do \(AH^2=BH\times HC\)

\(\Leftrightarrow AH^2=9\times16\)

\(\Leftrightarrow AH^2=144\)

\(\Leftrightarrow AH=\sqrt{144}\)

\(\Leftrightarrow AH=12\left(cm\right)\)

Áp dụng định lí Py-ta-go cho tam giác AHC vuông tại H ta được :

\(AH^2+HC^2=AC^2\)

\(\Leftrightarrow12^2+16^2=AC^2\)

\(\Leftrightarrow AC^2=400\)

\(\Leftrightarrow AC=\sqrt{400}\)

\(\Leftrightarrow AC=20\left(cm\right)\)

  Ta có : \(BC=BH+HC=9+16=25\left(cm\right)\)

Do BE là phân giác của \(\widehat{ABC}\)

\(\Rightarrow\frac{AE}{AB}=\frac{EC}{BC}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được :

\(\frac{AE}{AB}=\frac{EC}{BC}=\frac{AE+EC}{9+25}=\frac{AC}{34}=\frac{20}{34}=\frac{10}{17}\)

\(\Rightarrow\frac{EC}{BC}=\frac{10}{17}\Leftrightarrow\frac{EC}{25}=\frac{10}{17}\Leftrightarrow EC=\frac{250}{17}\left(cm\right)\)

Lại có : \(AE=AC-EC=20-\frac{250}{17}=\frac{90}{17}\left(cm\right)\)

Vậy độ dài đoạn thẳng EC là \(\frac{250}{17}\) cm ; AE là \(\frac{90}{17}\) cm

a: góc AIH=góc AKH=góc KAI=90 độ

=>AIHK là hcn

b: AIHK là hcn

=>góc AIK=góc AHK=góc C

=>ΔAIK đồng dạng với ΔACB

1. \(3x-15=2x\left(x-5\right)\)

\(\Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\)

\(\Leftrightarrow\left(x-5\right).\left(3-2x\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\3-2x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=5\\x=\frac{3}{2}\end{cases}}\)

Vậy \(S=\left\{5;\frac{3}{2}\right\}\)

a. Xét \(\Delta ABC\)và \(\Delta HAC\)có: 

Góc C: chung (gt)

Góc HAC = Góc ABC ( cùng phụ với góc ACB)

\(\Rightarrow\Delta ABC\infty\Delta HAC\)

b.Ta có:  \(\Delta ABC\infty\Delta HAC\)(cmt)

\(\Rightarrow\frac{BC}{AC}=\frac{AC}{HC}\Rightarrow AC^2=BC.HC=\left(BH+HC\right).HC=\left(9+12\right).12=252cm.\Rightarrow AC=\sqrt{252}=6\sqrt{7}\)

a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có 

\(\widehat{HBA}\) chung

Do đó: ΔHBA\(\sim\)ΔABC(g-g)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{15^2}+\dfrac{1}{20^2}=\dfrac{625}{90000}\)

\(\Leftrightarrow AH=12\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+BH^2\)

\(\Leftrightarrow BH^2=15^2-12^2=81\)

hay BH=9(cm)

Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:

\(AC^2=AH^2+CH^2\)

\(\Leftrightarrow CH^2=AC^2-AH^2=20^2-12^2=256\)

hay CH=16(cm)

c) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất đường phân giác của tam giác)

hay \(\dfrac{AD}{15}=\dfrac{CD}{25}=\dfrac{AD+CD}{15+25}=\dfrac{20}{40}=\dfrac{1}{2}\)

Do đó: AD=7,5cm; CD=12,5cm

Xét ΔABC vuông tại A và ΔHAC vuông tại H có

góc C chung

=>ΔABC đồng dạng với ΔHAC

BA^2=HB*HC

=>HB(HB+10,8)=7,2^2

=>HB^2+10,8HB-7,2^2=0

=>HB=3,6cm

=>BC=14,4cm

\(AC=\sqrt{14.4^2-7.2^2}=\dfrac{36}{5}\sqrt{3}\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}\cdot\dfrac{36\sqrt{3}}{5}\cdot7.2\simeq44,89\left(cm^2\right)\)