mik đang cần gáp bài này mn giúp mik với

Số đo góc ngoài đỉnh C là:

\(180^0-71^0=109^0\)

Số đo góc D là: 360^o - 65^o - 117^o - 68^o = 110^o

Số đo góc ngoài đỉnh D: 180^o - 110^o = 70^o

Số đo góc ngoài tại đỉnh D là:

\(180^0-\left(360^0-65^0-117^0-68^0\right)=70^0\)

D

D nhá!!!!:))

D

Chọn C

Số đo góc ngoài tại đỉnh B là:

\(180^0-360^0+57^0+110^0+75^0=62^0\)

Đáp án cần chọn là: C

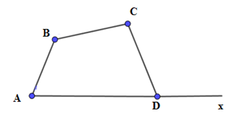
C D x ^ là góc ngoài đỉnh D.

Tứ giác ABCD có:  D ^ = 360 ° - A ^ + B ^ + C ^ = 360 ° - 65 ° + 117 ° + 71 ° = 107 °

Vì  A D C ^ và  C D x ^ là hai góc kề bù nên

C D x ^ = 180 ° - D ^ = 180 ° - 107 ° = 73 °

Ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{0}\)(Định lí tổng các góc trong tứ giác)

\(\Rightarrow\)\(\widehat{D}=360^{0}-(\widehat{A}+\widehat{B}+\widehat{C})\)

\(=360^{0}-(65^{0}+117^{0}+71^{0}) =107^{0}\)

Gọi \(\widehat{D_{1}}\) là góc ngoài tại đỉnh D của tứ giác ABCD. Ta có:

\(\widehat{D}+\widehat{D_{1}}=180^{0}\) (\(\widehat{D}\) và \(\widehat{D_{1}}\) là hai góc kề bù)

\(\Rightarrow\) \(\widehat{D_{1}}=180^{0}-\widehat{D}\)

\(=180^{0}-107^{0}=73^{0}\)

Vậy số đo góc ngoài tại đỉnh D của tứ giác ABCD là 73⁰

Tứ giác ABCD có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

\(65^o+117^o+71^o+\widehat{D}=360^o\)

\(253^o+\widehat{D}=360^o\)

\(\widehat{D}=360^o-253^o=107^o\)

\(\Rightarrow\) Góc ngoài của \(\widehat{D}=180^o-107^o=73^o\)

Vậy số đo góc ngoài tại đỉnh D là \(73^o\)

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^O\) (định lí tứ giác)\

\(\Rightarrow\widehat{D}=360^o-65^o-117^o-71^o\)

\(\Rightarrow\widehat{D}=107^o\)

Gọi \(\widehat{D_1}\) là góc ngoài tại đỉnh D của tứ giác ABCD

\(\Rightarrow\widehat{D}+\widehat{D_1}=180^o\) (kề bù)

\(\Rightarrow\widehat{D_1}=180^o-107^o\)

\(\Rightarrow\widehat{D_1}=73^o\)

Số đo góc ngoài tại đỉnh \(D\) là:  \(360^\circ  - \left( {65^\circ  + 100^\circ  + 60^\circ } \right) = 135^\circ \)