Bài 8c và bài 9 ạ

Những câu hỏi liên quan
Bài 7: Tính
b) 7/4 - 5/8
c) 9 x 3/11
d) 1/2 : 2/5
Trình bày rõ cách làm ra giúp em/mình ạ
7 / 4 - 5/8 = 14 / 8 - 5 / 8 = 9/8
9 / 1 . 3 / 11 = 27 / 11
1/2 . 5 / 2 = 5 / 4
Đúng 2
Bình luận (0)
\(\dfrac{7}{4}-\dfrac{5}{8}=\dfrac{14}{8}-\dfrac{5}{8}=\dfrac{9}{8}\)
\(9\times\dfrac{3}{11}=\dfrac{9\times3}{11}=\dfrac{27}{11}\)
\(\dfrac{1}{2}:\dfrac{2}{5}=\dfrac{1}{2}\times\dfrac{5}{2}=\dfrac{5}{4}\)
Đúng 1
Bình luận (0)
Bài 7: Tính
b) 7/4 - 5/8=7/4-5/8=14/8-5/8=9/8
c) 9 x 3/11=9/1.3/11=27/11
d) 1/2 : 2/5=1/2.5/2=5/4
Đúng 0
Bình luận (0)
a) 3^10 . (-5)^21 / (-5)^20 . 3^12
b) -11^5 . 13^7 / 11^5 . 13^8
c) 2^10 . 3^10 - 2^10 . 3^9 / 2^9 . 3^10
d) 5^11. 7^12 + 5^11 . 7^11/5^12 . 7^12 + 9 . 5^11 . 7^11
giúp em với ạ!! Đề bài là rút gọn ạ
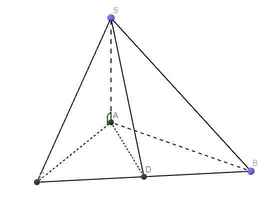
Giúp em câu 8c và câu 9 với ạ
9.
Gọi D là trung điểm BC \(\Rightarrow AD\perp BC\) (do tam giác ABC đều)
Mặt khác \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAD\right)\)
Mà BC là giao tuyến (SAB) và (SBC)
\(\Rightarrow\widehat{SDA}\) là góc giữa (ABC) và (SBC)
\(AD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{1}{\sqrt{3}}\)
\(\Rightarrow\widehat{SDA}=30^0\)
b.
Câu b nhìn không rõ, đề yêu cầu tính diện tích tam giác SBC đúng không nhỉ?
Từ câu a ta có \(BC\perp\left(SAD\right)\Rightarrow SD\perp BC\)
Pitago tam giác SAD: \(SD=\sqrt{SA^2+AD^2}=a\)
\(\Rightarrow S_{\Delta SBC}=\dfrac{1}{2}SD.BC=\dfrac{a^2}{2}\)
Đúng 0
Bình luận (0)
bài 9 : tìm số tự nhiên x, biết a,x in B(5) và 20 le x le 36 b, x in Ư (20) và x 8c, x ⋮ và 13 x le 78 d, 24 ⋮ và x là số chẵn
Đọc tiếp
bài 9 : tìm số tự nhiên x, biết
a,x \(\in\) B(5) và 20 \(\le\) x \(\le\) 36 b, x \(\in\) Ư (20) và x > 8
c, x \(⋮\) và 13 < x \(\le\) 78 d, 24 \(⋮\) và x là số chẵn
a: \(x\in B\left(5\right)\)
=>\(x\in\left\{0;5;10;15;20;25;30;35;40;...\right\}\)
mà 20<=x<=36
nên \(x\in\left\{20;25;30;35\right\}\)
b: \(x\inƯ\left(20\right)\)
=>\(x\in\left\{1;2;4;5;10;20\right\}\)
mà x>8
nên \(x\in\left\{10;20\right\}\)
Đúng 1
Bình luận (0)
Bài 1: Tính
a, 5/6 + 3/5
b, 11/16 - 5/8
c, 5/9 x 6/7
d, 5/4 : 3/4
giúp me
Bài 1: Tính
a, 5/6 + 3/5=40/30
b, 11/16 - 5/8=1/16
c, 5/9 x 6/7=30/63
d, 5/4 : 3/4=5/3
giúp me
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mấy bạn giải giúp mik bài 7 và bài 9 vs ạ
Bài 7:
a)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge m+1\\x\ge\dfrac{m}{4}\end{matrix}\right.\)
TH1: \(m+1< \dfrac{m}{4}\Rightarrow m< -\dfrac{4}{3}\)
\(\Rightarrow x\ge\dfrac{m}{4}\)\(\Rightarrow x\in\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
\(\Leftrightarrow\dfrac{m}{4}\ge0\Leftrightarrow m\ge0\) kết hợp với \(m< -\dfrac{4}{3}\Rightarrow m\in\varnothing\)
TH2:\(m+1\ge\dfrac{m}{4}\Rightarrow m\ge-\dfrac{4}{3}\)
\(\Rightarrow x\ge m+1\)\(\Rightarrow\)\(x\in\)\([m+1;+\)\(\infty\))
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([m+1;\)\(+\infty\)\()\)
\(\Leftrightarrow m+1\le0\Leftrightarrow m\le-1\) kết hợp với \(m\ge-\dfrac{4}{3}\)
\(\Rightarrow m\in\left[-\dfrac{4}{3};-1\right]\)
Vậy...
b)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge2-m\\x\ne-m\end{matrix}\right.\)\(\Rightarrow x\in\)\([2-m;+\)\(\infty\)) (vì \(-m< 2-m\))
Để hàm số xác ddingj với mọi x dương
\(\Leftrightarrow\left(0;+\infty\right)\subset\)\([2-m;+\)\(\infty\))
\(\Leftrightarrow2-m\le0\Leftrightarrow m\ge2\)
Vậy...
Đúng 2
Bình luận (0)
Bài 9:
a)Đặt \(f\left(x\right)=x^2+2x-2\)
TXĐ:\(D=R\)
TH1:\(x\in\left(-\infty;-1\right)\)
Lấy \(x_1;x_2\in\left(-\infty;-1\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2\)
Vì \(x_1;x_2\in\left(-\infty;-1\right)\Rightarrow x_1+x_2< -1+-1=-2\)\(\Leftrightarrow x_1+x_2+2< 0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;-1\right)\)
TH2:\(x\in\left(-1;+\infty\right)\)
Lấy \(x_1;x_2\in\left(-1;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2>0\)
Suy ra hàm đb trên \(\left(-1;+\infty\right)\)
Vậy...
b)Đặt \(f\left(x\right)=\dfrac{2}{x-3}\)
TXĐ:\(D=R\backslash\left\{3\right\}\)
TH1:\(x\in\left(-\infty;3\right)\)
Lấy \(x_1;x_2\in\left(-\infty;3\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(-\infty;3\right)\Rightarrow x_1-3< 0;x_2-3< 0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;3\right)\)
TH2:\(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(3;+\infty\right)\Rightarrow x_1-3>0;x_2-3>0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(3;+\infty\right)\)
Vậy hàm nb trên \(\left(-\infty;3\right)\) và \(\left(3;+\infty\right)\)
Đúng 2
Bình luận (0)
Mọi người giúp mình bài 8 và bài 9 câu a với ạ 
8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
Đúng 1
Bình luận (0)
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
Có ai có các câu họi tự luận bài 44 sinh 9 và bài 47 ko ạ cho em xin với ạ.Em cảm ơn ạ!!!
bài 1bài 2 bài 3 bài 4 bài 5 bài 6bài 7 bài 8 bài 9 gấp ạ !!! , nhanh tick cho ạ
Đọc tiếp
bài 1
bài 2

bài 3
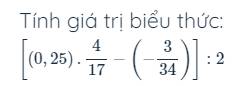
bài 4
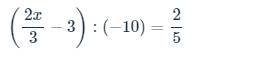
bài 5
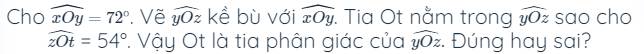
bài 6
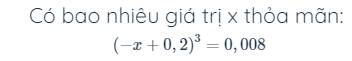
bài 7
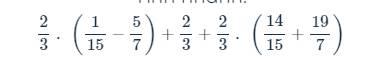
bài 8

bài 9
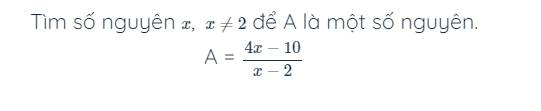
gấp ạ !!! , nhanh tick cho ạ
Bài 9:
Để A là số nguyên thì \(4x-10⋮x-2\)
=>\(4x-8-2⋮x-2\)
=>\(-2⋮x-2\)
=>\(x-2\inƯ\left(-2\right)\)
=>\(x-2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{3;1;4;0\right\}\)
Bài 8:
Diện tích mảnh vườn là:
\(\dfrac{1}{2}\cdot10\cdot\left(15+25\right)=5\cdot40=200\left(m^2\right)\)
Khối lượng thóc thu được là:
\(200:1\cdot0,7=140\left(kg\right)\)
Bài 7:
\(\dfrac{2}{3}\cdot\left(\dfrac{1}{15}-\dfrac{5}{7}\right)+\dfrac{2}{3}+\dfrac{2}{3}\cdot\left(\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{1}{15}-\dfrac{5}{7}+1+\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(1+1+2\right)\)
\(=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\)
Bài 6:
\(\left(-x+0,2\right)^3=0,008\)
=>\(-x+0,2=\sqrt[3]{0,008}=0,2\)
=>-x=0
=>x=0
=>Có 1 giá trị x thỏa mãn
Câu 4:
\(\left(\dfrac{2x}{3}-3\right):\left(-10\right)=\dfrac{2}{5}\)
=>\(x\cdot\dfrac{2}{3}-3=\dfrac{2}{5}\cdot\left(-10\right)=-4\)
=>\(x\cdot\dfrac{2}{3}=-4+3=-1\)
=>\(x=-1:\dfrac{2}{3}=-\dfrac{3}{2}\)
Đúng 0
Bình luận (0)