8c.
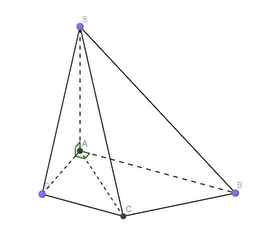
Do \(SA\perp\left(ABCD\right)\Rightarrow\) AD là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
Tương tự ta có AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{3}}{\sqrt{2}}\Rightarrow\widehat{SCA}\approx50^046'\)
Đúng 0
Bình luận (0)
Mọi người giúp em với. Làm từ tối đến giờ chưa ra. :'(
