Những câu hỏi liên quan
Cho tứ giác ABCD. I là điểm chính giữa cạnh AB. Biết diện tích tam giác ACD và BCD lần lượt là 12 cm2 và 18 cm2. Tính diện tích tam giác DIC.
Không có hình, tao khó hình dung ra được cái đề của mày.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có CD 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính côtang của góc giữa hai mặt phẳng (ACD) và (BCD). A.
3
4
B.
3
5
C.
5
3
D.
4
3
Đọc tiếp
Cho tứ diện ABCD có CD = 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính côtang của góc giữa hai mặt phẳng (ACD) và (BCD).
A. 3 4
B. 3 5
C. 5 3
D. 4 3
Cho tứ diện ABCD có CD 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính cotan của góc giữa hai mặt phẳng (ACD) và (BCD)? A.
3
4
B.
3
5
C.
5
3
D.
4
3
Đọc tiếp
Cho tứ diện ABCD có CD = 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính cotan của góc giữa hai mặt phẳng (ACD) và (BCD)?
A. 3 4
B. 3 5
C. 5 3
D. 4 3
Đáp án D
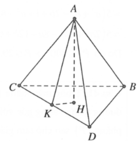
Gọi H là hình chiếu của A trên (BCD) ⇒ A H ⊥ B C D
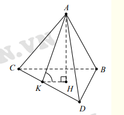 Kẻ
H
K
⊥
C
D
K
∈
C
D
⇒
C
D
⊥
A
H
K
⇒
A
C
D
;
B
C
D
^
=
A
K
H
^
Kẻ
H
K
⊥
C
D
K
∈
C
D
⇒
C
D
⊥
A
H
K
⇒
A
C
D
;
B
C
D
^
=
A
K
H
^
Ta có V A B C D = 1 3 A H . S ∆ B C D ⇒ A H = 3 V S ∆ B C D = 3 . 20 10 = 6
Và S ∆ A C D = 1 2 A K . C D ⇒ A K = 2 . S C D = 2 . 15 3 = 10
Tam giác AHK vuông tại H, có c o t A K H ^ = H K A H = 10 2 - 6 2 6 = 4 3
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có diện tích 47cm2 cạnh CB kéo dài về phía B cạnh DA kéo dài về phía A chúng cắt nhau tại I. Biết diện tích tam giác ABC và BCD là 12cm2 và 24cm2. Tính diện tích tam giác AIB.
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi
G
1
;
G
2
;
G
3
G
4
lần lượt là trọng tâm các tam giác ABC;ABD;ACD; và BCD. Biết
A
B
6
a
;
A
C
9
a
;
A
D
12
a
. Tính theo a thể tích khối tứ diện
G
1...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi G 1 ; G 2 ; G 3 G 4 lần lượt là trọng tâm các tam giác ABC;ABD;ACD; và BCD. Biết A B = 6 a ; A C = 9 a ; A D = 12 a . Tính theo a thể tích khối tứ diện G 1 G 2 G 3 G 4 .
A. 4 a 3
B. a 3
C. 108 a 3
D. 36 a 3
Gọi I, J, K lần lượt là trung điểm của BD, CD, BC.
Thể tích khối tứ diện vuông ABCD là:
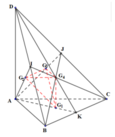
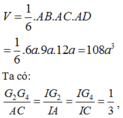
tương tự:
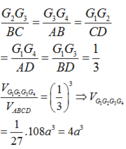
Chọn: A
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)
a) Hãy xác định điểm L.
b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD.
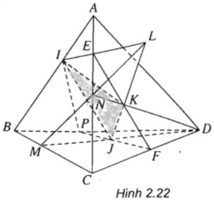
a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)
Đúng 0
Bình luận (0)
cho tam giác ABC có cạnh AC=AB .Kẻ đường cao BH và CK lần lượt xuống đáy ACvà AB .Hỏi
A.So sánh đọ dài CKvà BH
B.Trên cạnh AC kéo dài về phía C lấy điểm D.Trên cạnh AB lấy điểm E sao cho CD bằng BE .So sánh diện tích tam giác CBE và diện tích tam giác BCD
C.Nối E với D cắt BC ở I . biết diện tích tam giác BIE là 12cm2 . tính diện tích tam giác BID
Bạn lưu ý là KÉO DÀI AC VỀ PHÍA C LẤY ĐIỂM D, còn cạnh AB không kéo dài, mà lấy trực tiếp điểm E trên AB. Sao cho CD bằng với BE nhé.
cho tam giác ABC có cạnh AC=AB .Kẻ đường cao BH và CK lần lượt xuống đáy ACvà AB .Hỏi
A.So sánh đọ dài CKvà BH
B.Trên cạnh AC kéo dài về phía C lấy điểm D.Trên cạnh AB lấy điểm E sao cho CD bằng BE .So sánh diện tích tam giác CBE và diện tích tam giác BCD
C.Nối E với D cắt BC ở I . biết diện tích tam giác BIE là 12cm2 . tính diện tích tam giác BID
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)
a) Hãy xác định điểm L
b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD
a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)

Đúng 0
Bình luận (0)