một hình chữ nhật có chu vi 20cm và diện tích 24cm3.tìm các kích thước hình chữ nhật đó
Tìm hai kích thước của hình chữ nhật, biết độ dài hai kích thước của hình chữ nhật đó là các số nguyên và số đo diện tích bằng số đo chu vi
Gọi chiều dài là a, chiều rộng là b
Ta có :
\(a.b=2\left(a+b\right)\)
\(\Rightarrow2\left(a+b\right)-ab=0\)
\(2a+2b-ab=0\)
\(a\left(2-b\right)+2b=0\)
\(a\left(2-b\right)+2b-4=0-4\)
\(a\left(2-b\right)-2\left(2-b\right)=-4\)
\(\left(a-2\right)\left(b-2\right)=4\)
\(\Rightarrow a-2;b-2\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
Do \(a,b>0\) nên ta bỏ giá trị -4 và -2
Khoanh vào chữ đặt trước đáp án đúng:
Cho hình vuông và hình chữ nhật có kích thước như hình vẽ:
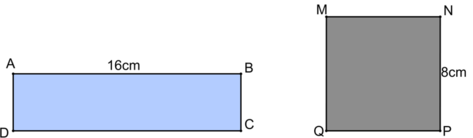
Biết rằng hình chữ nhật ABCD có diện tích bằng hình vuông MNPQ.
Chu vi hình chữ nhật ABCD là:
A. 32cm
B. 24cm
C. 20cm
D. 40cm.
Hướng dẫn giải:
Khoanh vào D. 40cm.
Giải thích:
Diện tích hình vuông (hình chữ nhật) là:
8 x 8 = 64 ( c m 2 )
Chiều rộng hình chữ nhật là:
64 : 16 = 4 (cm)
Chu vi hình chữ nhật là:
(16 + 4) x 2 = 40 (cm)
tìm các kích thước của 1 hình chữ nhật biết rằng chu vi hình chữ nhật là 38m và nếu tăng chiều dài thêm 2m và giảm chiều rộng đi 1m thì diện tích hình chữ nhật đó là 6m vuông
Sửa đề: Diện tích hình chữ nhật đó giảm đi 6m vuông
Gọi chiều dài, chiều rộng lần lượt là a,b
Nửa chu vi hình chữ nhật là 38/2=19
=>a+b=19
Theo đề, ta có hệ phương trình:
a+b=19 và (a+2)(b-1)=ab-19
=>a+b=19 và -a+2b=-17
=>a=55/3 và b=2/3
Một hình chữ nhất có chu vi là 134m. nếu giảm mỗi kích thước của vườn đi 1m thì diện tích của vườn bằng diện tích của hình vuông có cạnh bằng 28m. Tính các kích thước của hình chữ nhật đó.
Lời giải:
Gọi chiều dài và chiều rộng của hình chữ nhật là $a,b$ (m)
Theo bài ra ta có:
$a+b=134:2=67$
$(a-1)(b-1)=28^2=784$
$\Leftrightarrow ab-(a+b)+1=784$
$\Leftrightarrow ab-67+1=784$
$\Leftrightarrow ab=850$
Từ $a+b=67$ và $ab=850$ áp dụng định lý Viet đảo thì:
$a,b$ là nghiệm của pt:
$X^2-67X+850=0$
$\Rightarrow (a,b) = (50,17)$
Mà $a>b$ nên chiều dài là 50 m, chiều rộng là 17m
Một hình chữ nhật có chu vi là 160cm và diện tích là 1500 cm2 . Tính các kích thước còn lại của hình chữ nhật
Bài 179.Một hình chữ nhật có các kích thước là 30cm và 40cm. Người ta giảm bớt mỗi kích thước mỗi một hình đó x(cm) Gọi S và P thứ tự là diện tích và chu vi của hình chữ nhật mới theo x. a) Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao? b) Tính giá trị tương ứng của P khi x nhận các giá trị (tính theo đợn vị cm) sau: 0; 1; 2; 3; 4.
cứu em với huhu
a: \(S=\left(30-x\right)\left(40-x\right)\)
\(=\left(x-30\right)\left(x-40\right)=x^2-70x+1200\)
=>S không là hàm số bậc nhất đối với x
\(P=2\left[30-x+40-x\right]=2\left(70-2x\right)=-4x+140\)
=>P là hàm số bậc nhất đối với x
b: Khi x=0 thì \(P=-4\cdot0+140=140\)
Khi x=1 thì \(P=140-4=136\)
Khi x=2 thì \(P=140-8=132\)
Khi x=3 thì \(P=140-12=128\)
Khi x=4 thì P=140-4*4=124
một hình chữ nhật có chu vi 52m.nếu giảm mỗi cạnh 4m thì được hình chữ nhật mới có diện tích 77m2.tính các kích thước của hình chữ nhật ban đầu
Nửa chu vi của hình chữ nhật là:
52:2=26(m)
Gọi a(m) là chiều rộng ban đầu(Điều kiện: 0<a<26)
b(m) là chiều dài ban đầu(Điều kiện: 0<b<26)
(Điều kiện: \(a\le b\))
Vì nửa chu vi là 26m nên ta có phương trình: a+b=26(1)
Vì khi giảm mỗi cạnh 4m thì được hình chữ nhật mới có diện tích 77m2 nên ta có phương trình:
\(\left(a-4\right)\left(b-4\right)=77\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=26\\\left(a-4\right)\left(b-4\right)=77\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=26-b\\\left(26-b-4\right)\left(b-4\right)=77\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=26-b\\\left(-b+22\right)\left(b-4\right)=77\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=26-b\\-b^2+4b+22b-88-77=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=26-b\\b^2-26b+165=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=26-b\\\left(b-15\right)\left(b-11\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=26-b\\b-15=0\end{matrix}\right.\\\left\{{}\begin{matrix}a=26-b\\b-11=0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=11\\b=15\end{matrix}\right.\)
Vậy: Chiều rộng là 11m
Chiều dài là 15m
Một hình chữ nhật có kích thước là 20cm và 30cm ngta tăng mỗi kích thước thêm x (cm). Gọi y (cm) là chu vi hình chữ nhật mới
a) Hàm số thể hiện mối quan hệ của x và y là?
b) Khi chu vi hình chữ nhật mới là 120cm thì mỗi kích thước đã tăng bao nhiêu cm so với ban đầu?
Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của nó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.
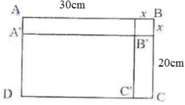
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)