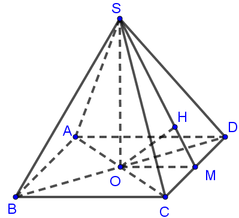
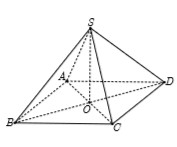
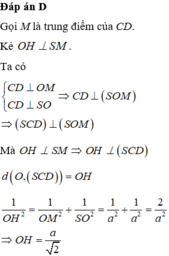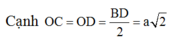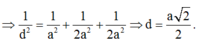58: Cho hình chóp đều S.ABCD, đáy ABCD là hình vuông tâm O.Khoảng cách từ O đến mặt đáy ABCD là

Những câu hỏi liên quan
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO a. Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
2
a
2
B.
3
a C.
5
a
5
D.
6...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 2 a 2
B. 3 a
C. 5 a 5
D. 6 a 3
Chọn A

Vẽ OE vuông góc CD, vẽ OH vuông góc với DE
Ta có
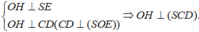
Tam giác vuông cân tại O, có
SO = OE = a
![]()
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO a. Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
3
a
B.
5
a
5
C.
6
a
3
D.
2
a
2
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 3 a
B. 5 a 5
C. 6 a 3
D. 2 a 2
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SOa (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
a
3
B.
a
5
5
C.
a
6
3
D.
a
2
2
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
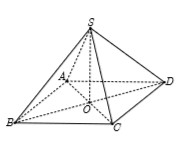
A. a 3
B. a 5 5
C. a 6 3
D. a 2 2
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO a (tham khảo hình vẽ bên)Khoảng cách từ O đến mặt phẳng (SCD) bằng A.
2
a
2
B.
3
a
C.
5
a
5
D.
6...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a (tham khảo hình vẽ bên)
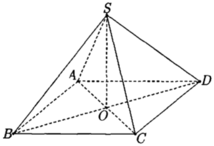
Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 2 a 2
B. 3 a
C. 5 a 5
D. 6 a 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SOa (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a (tham khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng (SCD) bằng
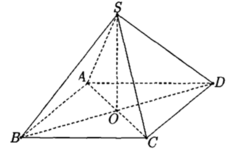
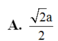
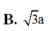
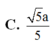
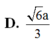
Cho hình chóp
S
.
A
B
C
D
có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên
S
A
a
2
và vuông góc với đáy (ABCD). Khoảng cách từ điểm B đến mặt phẳng (SCD) bằng A. a B.
a
3
C.
a
3
2
D.
a
6...
Đọc tiếp
Cho hình chóp S . A B C D có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên S A = a 2 và vuông góc với đáy (ABCD). Khoảng cách từ điểm B đến mặt phẳng (SCD) bằng
A. a
B. a 3
C. a 3 2
D. a 6 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O. Khoảng cách từ điểm O đến mặt phẳng (SCD) bằng
a
14
7
và góc giữa đường thẳng SB với mặt đáy bằng 60°. Tính thể tích V của khối chóp S.ABC theo a. A.
V
3
a
3
2
2...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O. Khoảng cách từ điểm O đến mặt phẳng (SCD) bằng a 14 7 và góc giữa đường thẳng SB với mặt đáy bằng 60°. Tính thể tích V của khối chóp S.ABC theo a.
A. V = 3 a 3 2 2
B. V = 3 a 3 2 4
C. V = 3 a 3 2 16
D. V = 9 a 3 2 4
cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a.Cạnh bên SA=acăn15/2 và vuông góc với mặt đáy (ABCD).Tính khoảng cách d từ O đến mp (SBC)
\(\left\{{}\begin{matrix}AO\cap\left(SBC\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SBC\right)\right)=2d\left(O;\left(SBC\right)\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{285}}{19}\)
\(\Rightarrow d\left(O;\left(SBC\right)\right)=\dfrac{1}{2}AH=\dfrac{a\sqrt{285}}{38}\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên \(SA=a\sqrt{3}\) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm A đến mặt phẳng (SBD).
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
Đúng 1
Bình luận (0)