Câu 3.
a) Tìm y :
y - \(\frac{1}{6}\)= \(\frac{5}{6}\)
b) Tính giá trị biểu thức:
1295 x 23 –16 839

Những câu hỏi liên quan
Cho biểu thức: P=\(\frac{a^6-2a^5+a-2}{a^5+1}\)
a) Rút gọn biểu thức P
b) Tính giá trị biểu thức P biết rằng \(\frac{a}{x+y}=\frac{5}{x+z}\)và \(\frac{25}{\left(x+z\right)^2}=\frac{16}{\left(z-y\right)\left(2x+y+z\right)}\)
Bài 1. Tìm GTNN của A.A frac{x^4+2x^3+8x+16}{x^4-2x^3+8x^2-8x+16} Bài 2. Rút gọn biểu thức và tính giá trị với x + y 2005P frac{xleft(x+5right)+yleft(y+5right)+2left(xy-3right)}{xleft(x+6right)+yleft(y+6right)+2xy}Bài 3. Cho ba0 và frac{a^2+b^2}{ab} frac{10}{3}Tính A frac{a-b}{a+b}
Đọc tiếp
Bài 1. Tìm GTNN của A.
A =\(\frac{x^4+2x^3+8x+16}{x^4-2x^3+8x^2-8x+16}\)
Bài 2. Rút gọn biểu thức và tính giá trị với x + y = 2005
P = \(\frac{x\left(x+5\right)+y\left(y+5\right)+2\left(xy-3\right)}{x\left(x+6\right)+y\left(y+6\right)+2xy}\)
Bài 3. Cho b>a>0 và \(\frac{a^2+b^2}{ab}\) = \(\frac{10}{3}\)
Tính A = \(\frac{a-b}{a+b}\)
\(P=\frac{x\left(x+5\right)+y\left(y+5\right)+2\left(xy-3\right)}{x\left(x+6\right)+y\left(y+6\right)+2xy}\)
\(=\frac{x^2+5x+y^2+5y+2xy-6}{x^2+6x+y^2+6y+2xy}\)
\(=\frac{\left(x+y\right)^2+5\left(x+y\right)-6}{\left(x+y\right)^2+6\left(x+y\right)}\)
\(=\frac{\left(x+y\right)\left(x+y+5\right)-6}{\left(x+y\right)\left(x+y+6\right)}\)
\(=\frac{2005\times\left(2005+5\right)-6}{2005\times\left(2005+6\right)}\)
\(=\frac{2005\times2010-6}{2005\times2011}\)
\(=\frac{2004}{2005}\)
Đúng 0
Bình luận (0)
Câu 1:
a) Tìm x, y, z biết: \(\frac{5z-6y}{4}=\frac{6x-4z}{5}=\frac{4y-5x}{6}\) và 3x - 2y + 5z = 96
b) Tìm giá trị nhỏ nhất của biểu thức: A = /x - 1/ + /x + 2020/
a) Ta có : \(\frac{5z-6y}{4}=\frac{6x-4z}{5}=\frac{4y-5x}{6}=\frac{20z-24y}{16}=\frac{30x-20z}{25}=\frac{24y-30x}{36}\)
\(=\frac{20z-24y+30x-20z+24y-30x}{16+25+36}=0\)
\(\Rightarrow\hept{\begin{cases}\frac{5z-6y}{4}=0\\\frac{6x-4z}{5}=0\end{cases}\Leftrightarrow\hept{\begin{cases}5z-6y=0\\6x-4z=0\end{cases}}\Leftrightarrow\hept{\begin{cases}5z=6y\\6x=4z\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{y}{5}=\frac{z}{6}\\\frac{z}{6}=\frac{x}{4}\end{cases}}}\)
\(\Leftrightarrow\frac{y}{5}=\frac{z}{6}=\frac{x}{4}=\frac{3x}{12}=\frac{2y}{10}=\frac{5z}{30}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{y}{5}=\frac{z}{6}=\frac{x}{4}=\frac{3x}{12}=\frac{2y}{10}=\frac{5z}{30}=\frac{3x-2y+5z}{12-10+30}=\frac{96}{32}=3\)
\(\Rightarrow\hept{\begin{cases}x=3.4=12\\y=3.5=15\\z=3.6=18\end{cases}}\)
thần đồng của năm đây rồi
Tính giá trị biểu thức:
A= \(\frac{\text{(a+1)(a+2)(a+3)....(a+2003)(a+2004) }}{(b+5)(b+6)(b+7)....(b+2006)(b+2007)}\) tại a= 0, b= -4
B= \(\frac{1}{\text{(x−5)(y+7) }}+\frac{1}{(x−4)(y+8)}+....+\frac{1}{(x−1)(y+11)}\)tại x= 6, y= -5
cho biểu thức \(P=\frac{a^6-2a^5+a-2}{a^5+1}...\)
a Rút gọn P
b tính giá trị của P biết \(\frac{a}{x+y}=\frac{5}{x+z}\)và \(\frac{25}{\left(x+z\right)^2}=\frac{16}{\left(z-y\right)\left(2x+y+z\right)}...\)
k mình mình giải chi tiết cho
Đúng 0
Bình luận (0)
Giải được nhưng mà lâu quá rồi giải làm gì nữa
Đúng 0
Bình luận (0)
Tìm các cặp số nguyên (a,b) sao cho: frac{b}{5}+frac{1}{10}frac{1}{a}Tìm các số hữu tỉ x, y, z thỏa mãn các điều kiện sau: x+yfrac{-7}{6}y+zfrac{1}{4}x+zfrac{1}{12}Tính giá trị các biểu thức sau:a)Afrac{frac{4}{5}-frac{4}{19}+frac{4}{23}}{frac{8}{5}-frac{8}{19}+frac{8}{23}}b)Bfrac{0,4-frac{2}{9}+frac{2}{11}}{1,4-frac{7}{9}+frac{7}{11}}-frac{frac{1}{3}-0,25+frac{1}{5}}{1frac{1}{6}-0,875+0,7}
Đọc tiếp
Tìm các cặp số nguyên (a,b) sao cho: \(\frac{b}{5}+\frac{1}{10}=\frac{1}{a}\)Tìm các số hữu tỉ x, y, z thỏa mãn các điều kiện sau: \(x+y=\frac{-7}{6}\)\(y+z=\frac{1}{4}\)\(x+z=\frac{1}{12}\)Tính giá trị các biểu thức sau:
a)\(A=\frac{\frac{4}{5}-\frac{4}{19}+\frac{4}{23}}{\frac{8}{5}-\frac{8}{19}+\frac{8}{23}}\)
b)\(B=\frac{0,4-\frac{2}{9}+\frac{2}{11}}{1,4-\frac{7}{9}+\frac{7}{11}}-\frac{\frac{1}{3}-0,25+\frac{1}{5}}{1\frac{1}{6}-0,875+0,7}\)
Cho hàm số y cot xa) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:xfrac{pi }{6}frac{pi }{4}frac{pi }{2}frac{{3pi }}{4}frac{{5pi }}{6}y cot x?????b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với x in left( {0;pi } right) và nối lại ta được đồ thị hàm số y cot x trên khoảng left( {0;pi } right) (Hình 31)c) Làm tương tự như trên đối với các khoảng left( {pi ;2pi } right),left( { -...
Đọc tiếp
Cho hàm số \(y = \cot x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
x | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(y = \cot x\) | ? | ? | ? | ? | ? |
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) (Hình 31)
c) Làm tương tự như trên đối với các khoảng \(\left( {\pi ;2\pi } \right),\left( { - \pi ;0} \right),\left( { - 2\pi ; - \pi } \right),....\)ta có đồ thị hàm số \(y = \cot x\)trên E được biểu diễn ở Hình 32.
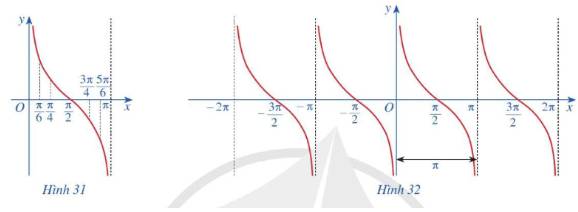
a)
x | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(y = \cot x\) | \(\sqrt 3 \) | 1 | 0 | -1 | \( - \sqrt 3 \) |
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) (Hình 31)
c) Làm tương tự như trên đối với các khoảng \(\left( {\pi ;2\pi } \right),\left( { - \pi ;0} \right),\left( { - 2\pi ; - \pi } \right),....\)ta có đồ thị hàm số \(y = \cot x\)trên E được biểu diễn ở Hình 32.
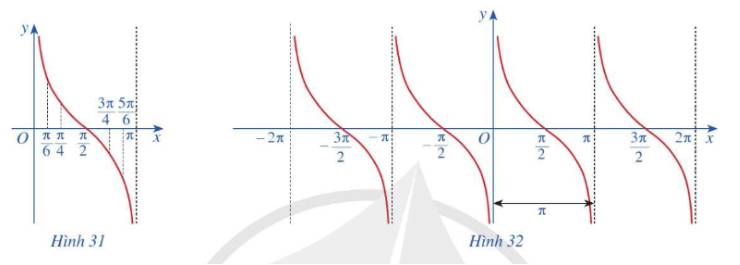
Đúng 0
Bình luận (0)
Câu 3:
Cho biểu thức: \(P=\left(\frac{x^2}{x^3-4x}+\frac{6}{6-3x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
a) Rút gọn P
b) Tính giá trị của biểu thức P khi /x/ =\(\frac{3}{4}\)
c)Với giá trị nào của x thì P=7
d) Tìm giá trị nguyên của x đẻ P có giá trị nguyên
\(ĐKXĐ:\hept{\begin{cases}x\ne\pm2\\x\ne0\end{cases}}\)
a) \(P=\left(\frac{x^2}{x^3-4x}+\frac{6}{6-3x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
\(\Leftrightarrow P=\left(\frac{x^2}{x\left(x-2\right)\left(x+2\right)}-\frac{6}{3\left(x-2\right)}+\frac{1}{x+2}\right):\frac{x^2-4+10-x^2}{x-2}\)
\(\Leftrightarrow P=\frac{x^2-2x\left(x+2\right)+x\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}:\frac{6}{x-2}\)
\(\Leftrightarrow P=\frac{x^2-2x^2-4x+x^2-2x}{x\left(x-2\right)\left(x+2\right)}\cdot\frac{x-2}{6}\)
\(\Leftrightarrow P=\frac{-6x}{6x\left(x+2\right)}\)
\(\Leftrightarrow P=\frac{-1}{x+2}\)
b) Khi \(\left|x\right|=\frac{3}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{4}\\x=-\frac{3}{4}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}P=-\frac{1}{\frac{3}{4}+2}=-\frac{4}{11}\\P=-\frac{1}{-\frac{3}{4}+2}=-\frac{4}{5}\end{cases}}\)
c) Để P = 7
\(\Leftrightarrow-\frac{1}{x+2}=7\)
\(\Leftrightarrow7\left(x+2\right)=-1\)
\(\Leftrightarrow7x+14=-1\)
\(\Leftrightarrow7x=-15\)
\(\Leftrightarrow x=-\frac{15}{7}\)
Vậy để \(P=7\Leftrightarrow x=-\frac{15}{7}\)
d) Để \(P\inℤ\)
\(\Leftrightarrow1⋮x+2\)
\(\Leftrightarrow x+2\inƯ\left(1\right)=\left\{\pm1\right\}\)
\(\Leftrightarrow x\in\left\{-3;-1\right\}\)
Vậy để \(P\inℤ\Leftrightarrow x\in\left\{-3;-1\right\}\)
Câu 1 : a) Tìm x in,biết |frac{1}{4}+ x | frac{5}{6}*Lưu ý : dấu | | là Giá trị tuyệt đối nha các cậu *b) Tính giá trị của biểu thức A 5x2 - 3x - 16 khi x -2 c) Cho đơn thức A4x2y2 ( -2x3y2) . Hãy thu gọn và chỉ ra hệ số,phần biến và bậc của đơn thức A HELP ME !!!!
Đọc tiếp
Câu 1 : a) Tìm x \(\in\),biết |\(\frac{1}{4}\)+ x | = \(\frac{5}{6}\)
*Lưu ý : dấu "| |" là Giá trị tuyệt đối nha các cậu *
b) Tính giá trị của biểu thức A = 5x2 - 3x - 16 khi x = -2
c) Cho đơn thức A=4x2y2 ( -2x3y2) . Hãy thu gọn và chỉ ra hệ số,phần biến và bậc của đơn thức A
HELP ME !!!!
a)\(\left|\frac{1}{4}+x\right|=\frac{5}{6}\)
=> Có hai trường hợp
TH1: \(\frac{1}{4}+x=\frac{5}{6}\) TH2: \(\frac{1}{4}+x=-\frac{5}{6}\)
<=> \(x=\frac{5}{6}-\frac{1}{4}\) <=> \(x=-\frac{5}{6}-\frac{1}{4}\)
<=> \(x=\frac{10}{12}-\frac{3}{12}\) <=> \(x=-\left(\frac{10}{12}+\frac{3}{12}\right)\)
<=> \(x=\frac{7}{12}\) <=> \(x=-1\frac{1}{12}\)
Vậy: \(x=\frac{7}{12}\) hoặc \(x=-1\frac{1}{12}\)
b) \(A\left(x\right)=5x^2-3x-16\)
Thay \(x=-2\) vào đa thức A(x), ta có:
\(A\left(-2\right)=5\cdot\left(-2\right)^2-3\cdot\left(-2\right)-16\)
\(A\left(-2\right)=5\cdot4-3\cdot\left(-2\right)-16\)
\(A\left(-2\right)=20+6-16\)
\(A\left(-2\right)=10\)
Vậy giá trị của đa thức A(x) tại x =-2 là 10
c) \(A=4x^2y^2\left(-2x^3y^2\right)\)
\(A=\left[4\cdot\left(-2\right)\right]\left(x^2\cdot x^3\right)\left(y^2\cdot y^2\right)\)
\(A=\left(-8\right)x^5y^4\)
Đơn thức A có:
- Hệ số là: -8
- Phần biến là: \(x^5y^4\)
- Bậc là: 9
Đúng 0
Bình luận (0)
a)
1/4+x=5/6 hoặc -5/6
1/4+x=5/6 suy ra x=7/12
1/4+x=-5/6 suy ra x=-13/12
b) thay x=-2 vào
suy ra A=5.(-2)2-3.(-2)-16
=10
c) A=-8x5y4. Hệ số -8. Biến x5y4. Bậc 9
Bài dễ sao ko động não tí đi
Đúng 0
Bình luận (0)
Câu 1: |1/4+x|=5/6
TH1: 1/4+x=5/6
x=5/6-1/4=7/12
TH2: 1/4+x=-5/6
x=-5/6-1/4=-13/12
Vậy x=7/12 hoặc x=-13/12
b) thay x=-2 ta có:
A=5.(-2)^2-3.(-2)-16
A=5.4-3.(-2)-16
A=20+6-16=10
c) A=4x^2y^2(-2x^3y^2)
A= (-2.4).(x^2x^3) (y^2y^2)=-8x^5y^4
Đơn thức A có hệ số là -8
phần biến là: x^5y^4
có bậc là:9
Bài này quá dễ
Đúng 0
Bình luận (0)





















