Hai đường thẳng cắt nhau tạo thành bốn góc (như trong hình vẽ).
Trong mỗi trường hợp sau, tính số đo $\widehat{O_4}$, biết
![]() $\widehat{O_1} - \widehat{O_2} = 70^{\circ}$;
$\widehat{O_1} - \widehat{O_2} = 70^{\circ}$;
![]() $\widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 325^{\circ}$.
$\widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 325^{\circ}$.
Cho hình vẽ. Tính các góc \(\widehat{O_1}\), \(\widehat{O_2}\), \(\widehat{O_3}\), \(\widehat{O_4}\)
Trong các trường hợp sau :
a) \(\widehat{O_1}+\widehat{O_2}=140^0\)
b) \(\widehat{O_1}+\widehat{O_3}=\widehat{O_2}+\widehat{O_4}\)
c) \(\widehat{O_2}-\widehat{O_1}=10^0\)
a: góc O1=góc O2=140/2=70 độ
góc O3=góc O4=180-70=110 độ
b: góc O1+góc O3=360/2=180 độ
góc O2+góc O4=180 độ
Góc O1 và O3 là hai góc kề bù rồi nên mặc nhiên tổng của hai góc đó bằng 180 độ nha bạn
Tương tự với cặp góc O2 và O4
=>Không tính được
c: góc O2=góc O1
nên góc O2-góc O1=10 độ là sai đề rồi bạn
Quan sát Hình 10.
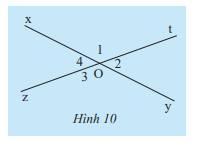
a) Hãy dùng thước đo góc để đo \(\widehat {{O_1}}\)và \(\widehat {{O_3}}\). So sánh số đo hai góc đó.
b) Hãy dùng thước đo góc để đo \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\). So sánh số đo hai góc đó.
Ta có:
\(\begin{array}{l}a)\widehat {{O_1}} = 135^\circ ;\widehat {{O_3}} = 135^\circ \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\\b)\widehat {{O_2}} = 45^\circ ;\widehat {{O_4}} = 45^\circ \Rightarrow \widehat {{O_2}} = \widehat {{O_4}}\end{array}\)
Cho Hình 3.51, trong đó Ox và Ox’ là hai tia đối nhau
a) Tính tổng số đo ba góc O1, O2, O3 .
Gợi ý: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\), trong đó \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {x'Oy}\)
b) Cho \(\widehat {{O_1}} = 60^\circ ,\widehat {{O_2}} = 70^\circ \). Tính \(\widehat {{O_2}}\)
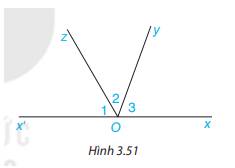
a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)
Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)
Vậy \(\widehat {{O_2}} = 50^\circ \)
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết \(\widehat {xOz} = 38^\circ \) (hình 6)
Tính số đo các góc \(\widehat {xOt},\widehat {tOy}\) và \(\widehat {yOz}\)
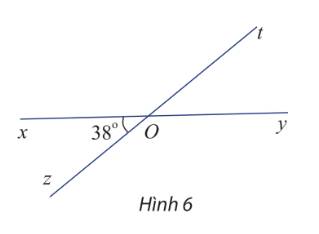
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)
Cho hai đường thẳng cắt nhau tại điểm O như hình vẽ (1).
a/Kể tên các cặp góc đối đỉnh trong hình vẽ bên (không kể tên góc bẹt)
b/Biết rằng \(\widehat{O_1}+\widehat{O_3}=110^o\).Hãy tính số đo các góc : \(\widehat{O_1};\widehat{O_2}\)
a, các cặp góc đối đỉnh là :
\(\widehat{O_1}\) và \(\widehat{O_3}\)
\(\widehat{O_2}\) và \(\widehat{O_4}\)
b, Ta có : \(\widehat{O_1}+\widehat{O_3}=110^0\)
Mà \(\widehat{O_1}\) đối đỉnh với \(\widehat{O_2}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}=\dfrac{110^0}{2}=55^0\)
\(\Rightarrow\widehat{O_1}+\widehat{O_2}=180^0\)
\(\Rightarrow\widehat{O_2}=180^0-55^0=125^0\)
Mà \(\widehat{O_2}\) đối đỉnh với \(\widehat{O_4}\)
\(\Rightarrow\widehat{O_2}=\widehat{O_4}=125^0\)
Cho đoạn thẳng AB. Vẽ hai tia Ax, By sao cho chúng tạo với AB hai góc so le trong có cùng số đo bằng 60\(^\circ \)(\(\widehat {xAB} = \widehat {yBA} = 60^\circ \)). Trên hình vừa vẽ, hai đường thẳng chứa hai tia Ax và By có song song với nhau không? Vì sao?
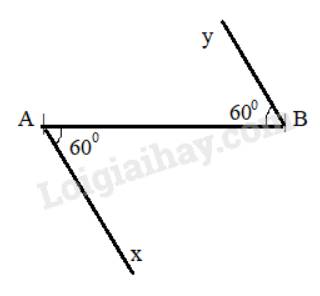
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành \(\widehat {PAM} = 33^\circ \) (Hình 9)
a) Tính số đo các góc còn lại.
b) Vẽ tia At là tia phân giác của \(\widehat {PAN}\). Hãy tính số đo của \(\widehat {tAQ}\). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của \(\widehat {MAQ}\)
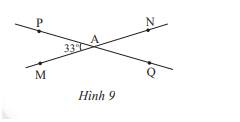
a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ - 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)
b)
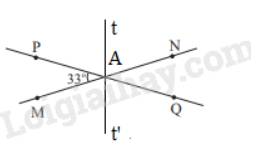
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ - 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)
Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)
Chú ý:
2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau
Xét các cặp góc đối đỉnh \(\widehat{_{A_1}}\)và \(\widehat{_{A_3}}\);\(\widehat{_{A_2}}\)và \(\widehat{A_4}\)được tạo thành khi hai đường thẳng a,b cắt nhau tại A .Tính số đo các góc \(_{A_1;A_2;A_3;A_4}\)trong mỗi trường hợp sau:
a) Góc A1+A3=\(120^O\)
b)\(3.\widehat{A_1}=7.\widehat{A_4}\)
Cho 5 đường thẳng cát nhau tại o
a, Có bao nhiêu góc trong hình vẽ
b, Trong các góc ấy có bao nhiêu góc đối đỉnh nhỏ hơn 180 độ
c, Xét các cặp góc đối đỉnh \(\widehat{A1}\)và \(\widehat{A3}\); \(\widehat{A2}\)và \(\widehat{A4}\)tạo thành hai đường thảng cắt nhau tại F
d, Tính số đo góc \(\widehat{A3}\); \(\widehat{A4}\)trong mỗi trường hợp sau
a, A1 + A2 = 100 độ
b, A1 - A2 = 100 độ
c, 2A1 = A4