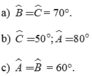Cho ai ko đọc đc câu hỏi thì:

a) cmr tam giác ABD = tam giác AEC

B) cm tứ giác BCDE là hình thang cân có đáy nhỏ bằng cạnh bên

C) cho góc A = 40 độ. Tính các góc còn lại của hình thang cân BCDE

a: Xét ΔABD và ΔACE có

góc ABD=góc ACE

AB=AC

góc BAD chung

=>ΔABD=ΔACE

b:ΔABD=ΔACE

=>AD=AE

Xét ΔABC có AE/AB=AD/AC

nên ED//BC

Xét tứ giác BEDC có

DE//BC

góc EBC=góc DCB

=>BEDC là hình thang cân

ED//BC

=>góc EDB=góc DBC

=>góc EDB=góc EBD

=>ED=EB

BEDC là hình thang cân

=>EB=DC

=>EB=ED=DC

c: góc EBC=góc DCB=(180-40)/2=70 độ

góc BED=góc EDC=180-70=110 độ

lỗi

Lỗi r bạn ;-;

Lỗi

Hình vẽ:

Lời giải:
a) 

Theo định lý tổng 3 góc trong tam giác:

$\widehat{D}+\widehat{E}+\widehat{F}=180^0$

$\Rightarrow \widehat{E}+\widehat{F}=180^0-\widehat{D}=180^0-60^0=120^0$

Mà tam giác $DEF$ cân tại $D$ nên $\widehat{E}=\widehat{F}$

Do đó:

$\widehat{E}=\widehat{F}=\frac{120^0}{2}=60^0$

b) 

Xét tam giác $ABM$ và $ACM$ có:

$AB=AC$ (do $ABC$ cân tại $A$)

$\widehat{B}=\widehat{C}$ (do $ABC$ cân tại $A$)

$BM=CM$ (do $M là trung điểm $BC$)

$\Rightarrow \triangle ABM=\triangle ACM$ (c.g.c)

a: góc ABC=góc ACB=(180-50)/2=65 độ

b: Xét ΔAMB và ΔANC có

AM=AN

góc BAM chung

AB=AC

=>ΔAMB=ΔANC

Answer:

a, 

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

Mà đề ra: \(\widehat{A}=40^o\)

\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A)

\(\Rightarrow40^o+\widehat{B}+\widehat{B}=180^o\)

\(\widehat{2B}=140^o\)

\(\widehat{B}=70^o\)

\(\Rightarrow\widehat{B}=\widehat{C}=70^o\)

b,

Theo đề ra: Tam giác ABC cân tại A

\(\Rightarrow\widehat{B}=\widehat{C}=50^o\)

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\widehat{A}+100^o=180^o\)

\(\Rightarrow\widehat{A}=80^o\)

c,

Theo đề ra: Tam giác ABC cân tại A

\(\Rightarrow\widehat{C}=\widehat{B}=60^o\)

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\widehat{A}+120^o=180^o\)

\(\Rightarrow\widehat{A}=60^o\)

a

b: \(\widehat{ACE}+\widehat{ACB}=90^0\)

mà \(\widehat{CAE}=180^0-90^0-\widehat{C}=90^0-\widehat{ACB}\)

nên \(\widehat{CAE}=\widehat{ACE}\)

hay ΔAEC cân tại E

a: \(\widehat{A}+\widehat{C}=180^0-30^0=150^0\)

\(\Leftrightarrow2\cdot\widehat{C}+90^0=150^0\)

\(\Leftrightarrow\widehat{C}=30^0\)

\(\Leftrightarrow\widehat{A}=120^0\)

cân tại A => goc C = goc B = 38 độ

góc A = 180 - goc C - góc B = 180 - 38 - 38 = 104 độ

Chúc ban hoc tot!

a> ta có : góc E = góc F = 40⁰ ( vì tam giác DEF cân tại D)

Tam giác DEF có : góc D+ góc E + góc F = 180⁰

                               góc D + 40⁰ +40⁰ = 180⁰

                               \(\Rightarrow\)góc D = 180⁰ - 40⁰-40⁰= 100⁰

b> Xét tam giác DEM và tam giác DFM có:

            AM : cạnh chung

           EDM = FDM( vì DM là phân giác của góc D)

           DE=DF ( vì tam giác DEF cân tại D)

Do đó : tam giác DEM = tam giác DFM ( c.g.c)

a) Xét tam giác DEF cân tại D có:

∠E=∠F= 40°(Tính chất của tam giác cân)

Ta có : ∠D+∠E+∠F=180°( Tổng 3 góc của 1 tam giác)

=>∠A+40°+40°=180°

    ∠A=180°-(40°+40°)

=> ∠A =100°

b)

GT: ΔDEF cân tại D

      DM là tia phân giác góc D

KL: ΔDEM=ΔDFM

Chứng minh:

Xét ΔDEM và ΔDFM có:

DM (cạnh chung)

∠D₁=∠D₂

DE=DF (ΔDEF cân )

=>ΔDEM = ΔDFM (c.g.c)