4x3-4x2-x+1=0
Giải pt
a. X4-4x3-6x2 -4x+1=0
b 4x2 +1/x2+7=8x+4/x
C 2x4+3x3 -16x2 +3x +2=0
a, \(x^4-4x^3-6x^2-4x+1=0\)(*)
<=> \(x^4+4x^2+1-4x^3-4x+2x^2-12x^2=0\)
<=> \(\left(x^2-2x+1\right)^2=12x^2\)
<=>\(\left(x-1\right)^4=12x^2\) <=> \(\left[{}\begin{matrix}\left(x-1\right)^2=\sqrt{12}x\\\left(x-1\right)^2=-\sqrt{12}x\end{matrix}\right.\)<=> \(\left[{}\begin{matrix}x^2-2x+1-\sqrt{12}x=0\left(1\right)\\x^2-2x+1+\sqrt{12}x=0\left(2\right)\end{matrix}\right.\)
Giải (1) có: \(x^2-2x+1-\sqrt{12}x=0\)
<=> \(x^2-2x\left(1+\sqrt{3}\right)+\left(1+\sqrt{3}\right)^2-\left(1+\sqrt{3}\right)^2+1=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2-3-2\sqrt{3}=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2=3+2\sqrt{3}\) <=> \(\left[{}\begin{matrix}x-1-\sqrt{3}=\sqrt{3+2\sqrt{3}}\\x-1-\sqrt{3}=-\sqrt{3+2\sqrt{3}}\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(ktm\right)\\x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(tm\right)\end{matrix}\right.\)
=> \(x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
Giải (2) có: \(x^2-2x+1+\sqrt{12}x=0\)
<=> \(x^2-2x\left(1-\sqrt{3}\right)+\left(1-\sqrt{3}\right)^2-\left(1-\sqrt{3}\right)^2+1=0\)
<=> \(\left(x+\sqrt{3}-1\right)^2=3-2\sqrt{3}\) .Có VP<0 => PT (2) vô nghiệm
Vậy pt (*) có nghiệm x=\(-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
Đố em tìm được giá trị của x để giá trị của phân thức 4 x 2 - 4 x 3 + x 4 x 3 - 2 x 2 bằng: 0
Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: 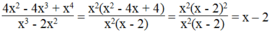
Nếu phân thức có giá trị bằng 0 thì biểu thức x - 2 cũng có giá trị bằng 0. Suy ra: x - 2 = 0 ⇒ x = 2 mà x = 2 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức có giá trị bằng 0.
Phân tích đa thức thành nhân tử :
a.x4 - 4x3 + 11x2 - 16x + 16
b.x4 + 6x3 + 13x2 + 12x + 4
c.x4 + x3 - 4x2 + x + 1
d.x4 + x3 - 4x2 + x + 1
c: \(x^4+x^3-4x^2+x+1\)
\(=x^4-x^3+2x^3-2x^2-2x^2+2x-x+1\)
\(=\left(x-1\right)\left(x^3+2x^2-2x-1\right)\)
\(=\left(x-1\right)\left[\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\right]\)
\(=\left(x-1\right)^2\cdot\left(x^2+3x+1\right)\)
tìm x biết 4x3+x=4x2
$4x^3 + x = 4x^2$
$\Leftrightarrow x(4x^2 - 4x + 1) = 0$
$\Leftrightarrow x(2x - 1)^2 = 0$
$\Leftrightarrow \left[\begin{aligned}&x = 0\\ &2x - 1 = 0\\ \end{aligned}\right. \Leftrightarrow \left[\begin{aligned}&x = 0\\ &x = \dfrac12\\ \end{aligned}\right.$
Thu gọn đa thức ( 5 x 3 + 4 x 2 - 1 ) - ( 4 x 3 - 4 x 2 + 1 ) ta được
A. 0
B. x 3 + 8 x 2 - 2
C. - x 3 + 8 x 2 - 2
D. - x 3 - 8 x 2 - 2
1) Thu gọn và sắp xếp các hạng của các đa thức sau theo lũy thừa giảm của các biến và chỉ rõ các hệ khác 0 của :
a, A(x)= 4+3x2-4x3+4x2-2x-x3+5x5
b, B(x)= x2+2x4+4x3-5x6+3x2-4x-1
2) Tính tổng và hiệu của 2 đa thức trên sau khi đã thu gọn
1: \(A=5x^5-5x^3+7x^2-2x+4\)
\(B\left(x\right)=-5x^6+2x^4+4x^3+4x^2-4x-1\)
2: \(A\left(x\right)+B\left(x\right)=5x^5-5x^3+7x^2-2x+4-5x^6+2x^4+4x^3+4x^2-4x-1\)
\(=-5x^6+5x^5+2x^4-x^3+11x^2-6x+3\)
\(A\left(x\right)-B\left(x\right)\)
\(=5x^5-5x^3+7x^2-2x+4+5x^6-2x^4-4x^3-4x^2+4x+1\)
\(=5x^6+5x^5-2x^4-9x^3+3x^2+2x+5\)
chứng minh các biểu thức sau ko phụ thuộc vào x
A, (2x+3)(4x2-6x+9)-2(4x3-1)
b, (4x3-1)-(4x-3)(16x2+3)
c, 2(x3y3)-3(x2y2)vs x+y=1
Cho
f ( x ) = x 2 + 2 x 3 - 7 x 5 - 9 - 6 x 7 + x 3 + x 2 + x 5 - 4 x 2 + 3 x 7 g ( x ) = x 5 + 2 x 3 - 5 x 8 - x 7 + x 3 + 4 x 2 - 5 x 7 + x 4 - 4 x 2 - x 6 - 12 h ( x ) = x + 4 x 5 - 5 x 6 - x 7 + 4 x 3 + x 2 - 2 x 7 + x 6 - 4 x 2 - 7 x 7 + x
Tính f(x) + g(x) – h(x)
chứng minh các biểu thức sau ko phụ thuộc vào x
A, (2x+3)(4x2-6x+9)-2(4x3-1)
b, (4x3-1)-(4x-3)(16x2+3)
c, 2(x3y3)-3(x2y2)vs x+y=1
Giúp mình vs ạ mình cảm ơn nhiều
a: Ta có: \(A=\left(2x+3\right)\left(4x^2-6x+9\right)-2\left(4x^3-1\right)\)
\(=8x^3+27-8x^3+2\)
=29
b: Ta có: \(B=\left(64x^3-1\right)-\left(4x-3\right)\left(16x^2+3\right)\)
\(=64x^3-1-64x^3-12x-48x^2+9\)
\(=-12x+8\)
c: Ta có: \(2\left(x^3+y^3\right)-3\left(x^2+y^2\right)\)
\(=2\left(x^2+xy+y^2\right)-3\left(-2xy\right)\)
\(=2x^2+2xy+2y^2+6xy\)
\(=2x^2+8xy+2y^2\)