\(\sqrt{ }\)(x2-1)-x=m
giải và biện luận phương trình trên:
Những câu hỏi liên quan
giải và biện luận phương trình:
\(\left(x-m\right)\sqrt{x-1}=x^2-m^2\)
Giải và biện luận phương trình sau: \(\frac{x}{\sqrt{x+m}}=\frac{x}{\sqrt{x+1}}\)
9 tháng 12 2021 lúc 17:26
Cho phương trình \(mx^2-2\left(m-1\right)x+m-3=0\)
Giải và biện luận phương trình trên.
Với \(m=0\)
\(PT\Leftrightarrow2x-3=0\Leftrightarrow x=\dfrac{3}{2}\)
Với \(m\ne0\)
\(\Delta'=\left(m-1\right)^2-m\left(m-3\right)=m+1\)
PT vô nghiệm \(\Leftrightarrow m+1< 0\Leftrightarrow m< -1\)
PT có nghiệm kép \(\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
\(\Leftrightarrow x=-\dfrac{b'}{a}=\dfrac{m-1}{2m}\)
PT có 2 nghiệm phân biệt \(\Leftrightarrow m+1>0\Leftrightarrow m>-1;m\ne0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{m-1+\sqrt{m+1}}{m}\\x=\dfrac{m-1-\sqrt{m+1}}{m}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho phương trình
|x+1| + m |x-1| = (m+1)\(\sqrt{x^2-1}\)
a, Giiari và biện luận phương trình đã cho
b, Giải phương trình khi m =2
giải và biện luận phương trình : \(\sqrt{x^2-1}-x=m\)
9B. Cho parabol (P) : y = 1/2 x^2
a) Vẽ (P) trên mặt phẳng tọa độ.
b) Dựa vào đồ thị hãy biện luận theo m số nghiệm của phương trình x2
– 2m + 4=0
giúp tui làm câu b ạ
a: 
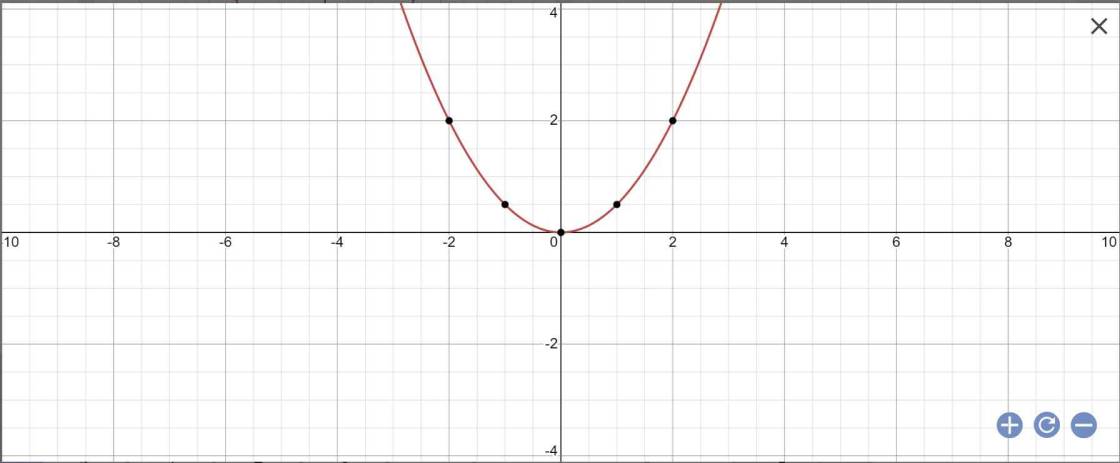
b: \(\Delta=\left(-2m\right)^2-4\cdot1\cdot4=4m^2-16\)
Để phương trình có hai nghiệm phân biệt thì 4m^2-16>0
=>m>2 hoặc m<-2
Để phương trình có nghiệm duy nhất thì 4m^2-16=0
=>m=2 hoặc m=-2
Để phương trìh vô nghiệm thì 4m^2-16<0
=>-2<m<2
Đúng 1
Bình luận (0)
16 tháng 3 2021 lúc 18:54
lập trình giải và biện luận phương trình bật hai:(m+1)x2-2x+2=0.
với m nhập từ bàn phím
+) Với \(m=-1\) phương trình trở thành :
\(-2x+2=0\Leftrightarrow x=1\)
+) Với \(m\ne-1\) Ta có :
\(\Delta'=\left(-1\right)^2-2\left(m+1\right)=-2m\)
+ Nếu \(m=0\Leftrightarrow\) pt có 2 nghiệm kép
+ Nếu \(m>0\Leftrightarrow\) pt vô nghiệm
+ Nếu \(m< 0\) pt có 2 nghiệm phân biệt
Vậy...
Đúng 1
Bình luận (0)
Cho hai phương trình x = 1 - 2mx (1) và m2x - m = 2x - \(\sqrt{2}\)(2)
a) Giải và biện luận phương trình (1) và (2)
b) Với giá trị nào của m thì 2 phương trình tương đương
Cho phương trình (m+2)x2−2(m−1)x+3−m=0 (1); với m là tham số thực
1) Giải và biện luận phương trình đã cho theo tham số m
2) Tìm m để phương (1) có hai nghiệm thỏa mãn tổng hai nghiệm bằng tích hai nghiệm.
1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)
\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)
\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)
\(=4m^2-8m+4+4m^2-4m-24\)
\(=-12m-20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow-12m-20>0\)
\(\Leftrightarrow-12m>20\)
hay \(m< \dfrac{-5}{3}\)
Để phương trình có nghiệm kép thì Δ=0
\(\Leftrightarrow-12m-20=0\)
\(\Leftrightarrow-12m=20\)
hay \(m=\dfrac{-5}{3}\)
Để phương trình vô nghiệm thì Δ<0
\(\Leftrightarrow-12m-20< 0\)
\(\Leftrightarrow-12m< 20\)
hay \(m>\dfrac{-5}{3}\)
Đúng 0
Bình luận (1)
2: ĐKXĐ: \(m\ne-2\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)
Suy ra: 2m-2=3-m
\(\Leftrightarrow2m+m=3+2\)
\(\Leftrightarrow3m=5\)
hay \(m=\dfrac{5}{3}\)(thỏa ĐK)
Đúng 0
Bình luận (0)