Cho tam giác ABC nhọn , G là trọng tâm , O là trực tâm . Chứng minh : tam giác ABC cân .
Cho tam giác nhọn ABC, H là trực tâm, G là trọng tâm, O là giao điểm các đường trung trực của tam giác. Chứng minh rằng: H, G, O thẳng hàng và HG=2GO
ho tam giác ABC nhọn . gọi H là trực tâm, O là giao điểm của 3 đường trung trực của tam giác đó.lấy điểm K sao cho O là trung điểm của AK.a) Chứng minh tứ giác BHCK là hình bình hành . b) vẽ trung tuyến AM cắt OH tại G. Chứng minh G là trọng tâm của tam giác ABC
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O và trực tâm H. Kẻ đường kính AD.
a/ Chứng minh tứ giác BHCD là hình bình hành
B/ Gọi I lầ trung điểm BC. Chứng minh: AH = 2OI
C/ Chứng minh: O,B là trọng tâm G của tam giác ABC là ba điểm thẳng hàng.
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO
Cho tam giác nhọn ABC , H là trục tâm , G là trọng tâm , O là giao điểm các đường trung trực của tam giác . Chứng minh rằng : H , G , O thẳng hàng và HG = 2GO
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, O là giao điểm ba đường trung trực của tam giác ABC. a) Tam giác BOC là tam giác gì? b) Chứng minh ba điểm A, O, G thẳng hàng?
Cho tam giác ABC nhọn nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC, I là trung điểm của BC và AD là đường kính, CH cắt AD tại E
a) Chứng minh AB.AE = AH.AC
b) AI cắt OH ở G. chứng minh G là trọng tâm tam giác ABC.
Cho tam giác ABC nhọn có ba đỉnh thuộc đường tròn (O). Gọi H là trực tâm của tam giác
ABC. Vẽ đường kính AD.
a) Tứ giác BHCK là hình gì?
b) Gọi I là trung điểm của BC. Chứng minh AH=2.OI
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh 3 điểm H, G, O thẳng hàng và GH=2.GO
d) So sánh diện tích hai tam giác AHG và tam giác AOG.
a) chắc đề hỏi là tứ giác BHCD là hình gì chứ ko có điểm K
Vì AD là đường kính \(\Rightarrow\left\{{}\begin{matrix}\angle ACD=90\\\angle ABD=90\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CD\bot AC\\BD\bot AB\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AB\end{matrix}\right.\Rightarrow\) \(CD\parallel BH,BD\parallel CH\) \(\Rightarrow BHCD\) là hình bình hành
b) Vì BHCD là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,D\) thẳng hàng và I cũng là trung điểm HD
Xét \(\Delta AHD\) có O là trung điểm AD,I là trung điểm HD
\(\Rightarrow OI\) là đường trung bình \(\Rightarrow OI=\dfrac{1}{2}AH\Rightarrow AH=2OI\)
c) AI cắt HO tại G'.
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{AH}{OI}=\dfrac{AG'}{G'I}\Rightarrow\dfrac{AG'}{G'I}=2\Rightarrow\dfrac{AG'}{AI}=\dfrac{2}{3}\)
\(\Rightarrow G'\) là trọng tâm tam giác ABC \(\Rightarrow G\equiv G'\Rightarrow\) đpcm
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{GH}{GO}=\dfrac{AH}{OI}=2\Rightarrow GH=2GO\)
d) Kẻ \(AF\bot HO\) \(\Rightarrow\left\{{}\begin{matrix}S_{AOG}=\dfrac{1}{2}.AF.OG\\S_{AHG}=\dfrac{1}{2}.AF.HG\end{matrix}\right.\)
mà \(GH=2GO\Rightarrow S_{AHG}=2S_{AOG}\)
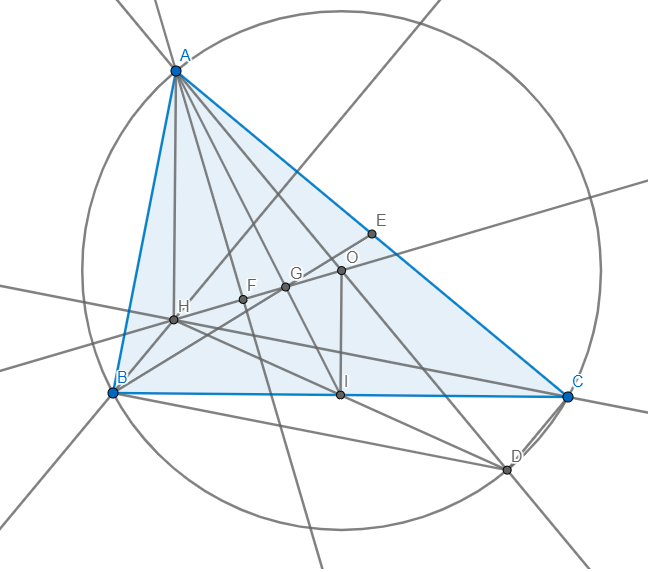
Cho tam giác ABC nhọn, H,G,O lần lượt là trực tâm, trọng tâm và giao của 3 đường trung trực của tam giác ABC, M là trung điểm của BC.
a, Chứng minh rằng OM=1/2 AH
b, E,F lần lượt là trung điểm của AG,HG
chứng minh: tam giác EFG = tam giác MOG
c, Chứng minh: H,G,O thẳng hàng
) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD
Xét Δ BCD có M là trung điểm BC, O là trung điểm CD OM là đường trung bình của Δ BCD
OM=12DB và OM // DB
mà OM⊥BC ( OM là đường trung trực của BC ) DB⊥BC
mà AH⊥BC( AH là đường cao của ΔABC ) AH // DB
Xét ΔABH và ΔBAD có
HABˆ=DBAˆ( 2 góc so le trong do AH // DB )
AB chung
ABHˆ=BADˆ( 2 góc so le trong do AH // DB )
ΔABH=ΔBAD( g-c-g )
AH = BD mà OM=12DB OM=12AH
AH = 2 OM ( đpcm )
b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A
Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A PQ là đường trung bình của \large\Delta AG'H
PQ=12AH và PQ // AH
Do PQ=12AH mà OM=12AH PQ = OM
Do AH // OM ( cùng ⊥BC ) mà PQ // AH PQ // OM
Xét ΔPQG′ và ΔOMG′ có
PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)
PQ = OM (c/m trên )
QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )
ΔPQG′=ΔOMG′( g-c-g )
G'Q = G'M và G'P = G'O
Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A ) G′M=12G′Amà G'M + G'A = AM
G′A=23AM mà AM là trung tuyến của ΔABC
G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC G′≡ G
mà G′∈OH G∈OH O, H, G thẳng hàng ( đpcm )
Hên xui nghe bạn ^ ^
Quyết Kiếm Sĩ:hên sui cái j copy trên mạng mà nổ wa :D
hình như Quyết kiếm sĩ sai rồi ấy
dòng 9 ấy
ho tam giác nhọn ABC có trực tâm H, O là giao điểm các trung trực của tam giác ABC. D là điểm sao cho O là trung điểm AD.
a) Chứng minh rằng tứ giác BHCD là hình bình hành.
b) Gọi M là trung điểm của BC. Chứng minh rằng AH=2OM.
c) Gọi G là trọng tâm của tam giác ABC. CMR: H,G,O thẳng hàng và OG=1/3OH