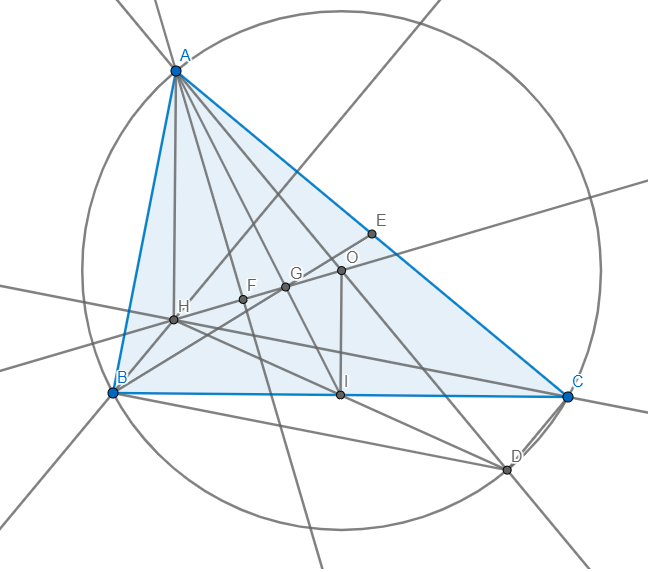
Cho tam giác ABC nhọn có ba đỉnh thuộc đường tròn (O). Gọi H là trực tâm của tam giác
ABC. Vẽ đường kính AD.
a) Tứ giác BHCK là hình gì?
b) Gọi I là trung điểm của BC. Chứng minh AH=2.OI
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh 3 điểm H, G, O thẳng hàng và GH=2.GO
d) So sánh diện tích hai tam giác AHG và tam giác AOG.
a) chắc đề hỏi là tứ giác BHCD là hình gì chứ ko có điểm K
Vì AD là đường kính \(\Rightarrow\left\{{}\begin{matrix}\angle ACD=90\\\angle ABD=90\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CD\bot AC\\BD\bot AB\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AB\end{matrix}\right.\Rightarrow\) \(CD\parallel BH,BD\parallel CH\) \(\Rightarrow BHCD\) là hình bình hành
b) Vì BHCD là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,D\) thẳng hàng và I cũng là trung điểm HD
Xét \(\Delta AHD\) có O là trung điểm AD,I là trung điểm HD
\(\Rightarrow OI\) là đường trung bình \(\Rightarrow OI=\dfrac{1}{2}AH\Rightarrow AH=2OI\)
c) AI cắt HO tại G'.
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{AH}{OI}=\dfrac{AG'}{G'I}\Rightarrow\dfrac{AG'}{G'I}=2\Rightarrow\dfrac{AG'}{AI}=\dfrac{2}{3}\)
\(\Rightarrow G'\) là trọng tâm tam giác ABC \(\Rightarrow G\equiv G'\Rightarrow\) đpcm
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{GH}{GO}=\dfrac{AH}{OI}=2\Rightarrow GH=2GO\)
d) Kẻ \(AF\bot HO\) \(\Rightarrow\left\{{}\begin{matrix}S_{AOG}=\dfrac{1}{2}.AF.OG\\S_{AHG}=\dfrac{1}{2}.AF.HG\end{matrix}\right.\)
mà \(GH=2GO\Rightarrow S_{AHG}=2S_{AOG}\)