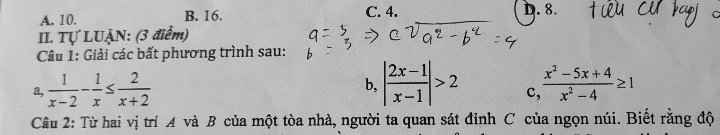
a: =>\(\dfrac{x-x+2}{x\left(x-2\right)}-\dfrac{2}{x+2}< =0\)

=>\(\dfrac{2}{x\left(x-2\right)}-\dfrac{2}{x+2}< =0\)

=>\(\dfrac{2x+4-2x^2+4x}{x\left(x-2\right)\left(x+2\right)}< =0\)

=>\(\dfrac{-x^2+3x+4}{x\left(x-2\right)\left(x+2\right)}< =0\)

=>\(\dfrac{\left(x-4\right)\left(x+1\right)}{x\left(x-2\right)\left(x+2\right)}>=0\)

TH1: (x-4)(x+1)>=0 và x(x-2)(x+2)>0

=>(x>=4 hoặc x<=-1) và (-2<x<0 hoặc x>2)

=>x>=4 hoặc -2<x<=-1

TH2: (x-4)(x+1)<=0 và x(x^2-4)<0

=>(-1<=x<=4) và (x<-2 hoặc 0<x<2)

=>0<x<2

b: =>(2x-1)/(x-1)>2 hoặc (2x-1)/(x-1)<-2

=>(2x-1-2x+2)/(x-1)>0 hoặc (2x-1+2x-2)/(x-1)<0

=>1/(x-1)>0 hoặc (4x-3)/(x-1)<0

=>x>1 hoặc 3/4<x<1

c: =>\(\dfrac{x^2-5x+4-x^2+4}{x^2-4}>=0\)

=>\(\dfrac{-5x+8}{x^2-4}>=0\)

=>\(\dfrac{5x-8}{x^2-4}< =0\)

TH1: 5x-8>=0 và x^2-4<0

=>x>=8/5 và -2<x<2

=>Loại

TH2: 5x-8<=0 và x^2-4>0

=>x<=8/5 và (x>2 hoặc x<-2)

=>x<-2

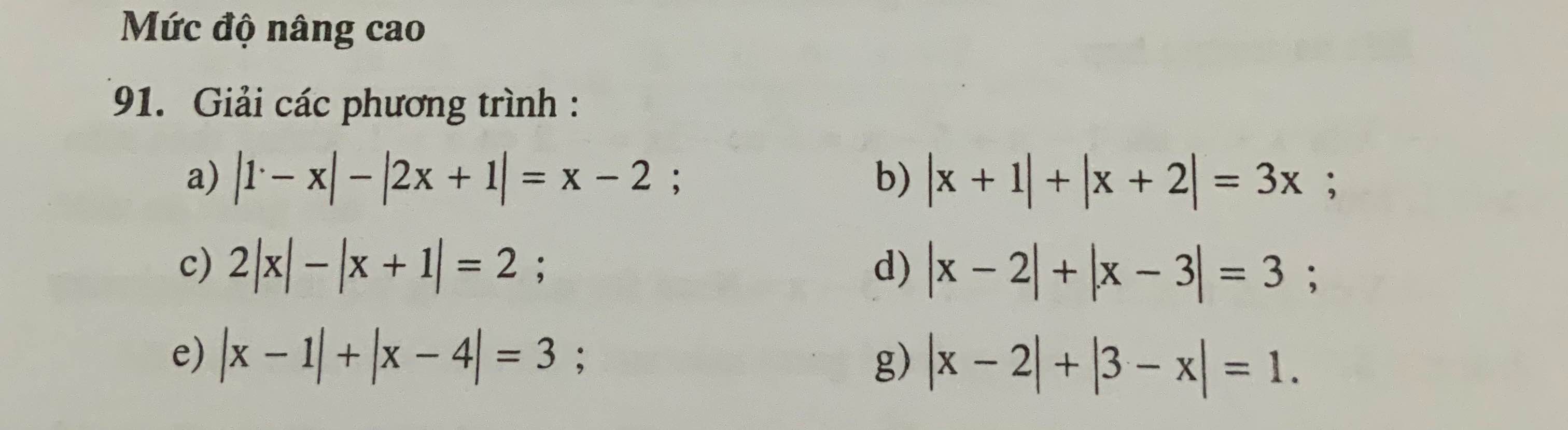
a: |1-x|-|2x+1|=x-2

=>|x-1|-|2x+1|=x-2(1)

TH1: x<-1/2

Phương trình (1) sẽ tương đương với:

1-x-(-2x-1)=x-2

=>1-x+2x+1=x-2

=>x+2=x-2

=>2=-2(vô lý)

=>\(x\in\varnothing\)

TH2: \(-\dfrac{1}{2}< =x< 1\)

Phương trình (1) sẽ trở thành:

\(1-x-\left(2x+1\right)=x-2\)

=>1-x-2x-1=x-2

=>-3x=x-2

=>-4x=-2

=>\(x=\dfrac{1}{2}\left(nhận\right)\)

TH3: x>=1

Phương trình (1) sẽ trở thành:

\(x-1-\left(2x+1\right)=x-2\)

=>x-1-2x-1=x-2

=>-x-2=x-2

=>-2x=0

=>x=0(loại)

b: \(\left|x+1\right|+\left|x+2\right|=3x\left(2\right)\)

TH1: x<-2

Phương trình (2) sẽ trở thành:

-x-1+(-x-2)=3x

=>\(3x=-2x-3\)

=>\(5x=-3\)

=>\(x=-\dfrac{3}{5}\left(loại\right)\)

TH2: -2<=x<-1

Phương trình (2) sẽ trở thành:

\(-x-1+x+2=3x\)

=>3x=1

=>\(x=\dfrac{1}{3}\left(loại\right)\)

TH3: x>=-1

Phương trình (2) sẽ trở thành:

\(x+1+x+2=3x\)

=>3x=2x+3

=>x=3(nhận)

c: \(2\left|x\right|-\left|x+1\right|=2\left(3\right)\)

TH1: x<-1

Phương trình (3) sẽ trở thành:

-2x-(-x-1)=2

=>-2x+x+1=2

=>-x+1=2

=>-x=1

=>x=-1(loại)

TH2: -1<=x<0

Phương trình (3) sẽ trở thành:

\(-2x-\left(x+1\right)=2\)

=>-2x-x-1=2

=>-3x=3

=>x=-1(nhận)

TH3: x>=0

Phương trình (3) sẽ trở thành:

\(2x-\left(x+1\right)=2\)

=>x-1=2

=>x=3(nhận)

d: \(\left|x-2\right|+\left|x-3\right|=3\left(4\right)\)

TH1: x<2

Phương trình (4) sẽ trở thành:

2-x+3-x=3

=>5-2x=3

=>2x=2

=>x=1(nhận)

Th2: 2<=x<3

Phương trình (4) sẽ trở thành:

\(x-2+3-x=3\)

=>1=3(loại)

Th3: x>=3

Phương trình (4) sẽ trở thành:

x-2+x-3=3

=>2x-5=3

=>2x=8

=>x=4(nhận)

e: |x-1|+|x-4|=3(5)

TH1: x<1

Phương trình (5) sẽ trở thành:

1-x+4-x=3

=>5-2x=3

=>2x=2

=>x=1(loại)

TH2: 1<=x<4

Phương trình (5) sẽ trở thành:

x-1+4-x=3

=>3=3(luôn đúng)

TH3: x>=4

Phương trình (5) sẽ trở thành:

x-1+x-4=3

=>2x-5=3

=>2x=8

=>x=4(nhận)

g: |x-2|+|3-x|=1

=>|x-2|+|x-3|=1(6)

TH1: x<2

Phương trình (6) sẽ trở thành:

2-x+3-x=1

=>5-2x=1

=>2x=4

=>x=2(loại)

TH2: 2<=x<3

Phương trình (6) sẽ trở thành:

x-2+3-x=1

=>1=1(luôn đúng)

TH3: x>=3

Phương trình (6) sẽ trở thành:

x-2+x-3=1

=>2x-5=1

=>2x=6

=>x=3(nhận)

Xe máy thứ nhất 1 giờ đi được 1/4 quảng đường

Xe máy thứ hai 1 giờ đi được 1/3 quảng đường

Sau 1,5 giờ 2 xe đi được:(1/4+1/3)x1,5=7/12x3/2=7/8(quảng đường)

quảng đường AB là:

15x8=120(km)

Xem lại đề đi bạnn

Trả lời đúng giúp mình.

Bài 2 :

a, Ta có : \(x^2-5x+4< 0\)

\(\Leftrightarrow x^2-x-4x+4< 0\)

\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)< 0\)

\(\Leftrightarrow\left(x-4\right)\left(x-1\right)< 0\)

Vậy ...

b, Ta có : \(\dfrac{x-3}{x+1}< 1\)

\(\Leftrightarrow\dfrac{x-3}{x+1}-\dfrac{x+1}{x+1}< 0\)

\(\Leftrightarrow\dfrac{x-3-x-1}{x+1}=\dfrac{-4}{x+1}< 0\)

Thấy - 4 < 0

Nên để \(-\dfrac{4}{x+1}< 0\) <=> x + 1 > 0 ( TH A, B trái dấu )

Vậy ...

Bài 1: 

a) ĐKXĐ: \(x\ge2\)

Ta có: \(3\sqrt{x-2}+\sqrt{25x-50}=2^5\)

\(\Leftrightarrow3\sqrt{x-2}+5\sqrt{x-2}=32\)

\(\Leftrightarrow8\sqrt{x-2}=32\)

\(\Leftrightarrow\sqrt{x-2}=4\)

\(\Leftrightarrow x-2=16\)

hay x=18(thỏa ĐK)

Vậy: S={18}

Điều kiện: \(x\ge-1\)

PT \(\Rightarrow-2x-2\le x^2-2x-3\le2x+2\)

+) Xét \(x^2-2x-3\ge-2x-2\) \(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\)

+) Xét \(x^2-2x-3\le2x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge5\end{matrix}\right.\)

 \(\Rightarrow x\in(-\infty;-1]\cup[-5;+\infty)\)

Đăng nhập vào Gmail của bạn, nhấn chuột vào biểu tượng bánh răng ở góc trên bên phải. Từ menu xổ xuống > Chọn Settings.

Khi màn hình cài đặt mở ra, nó sẽ hiển thị tab General theo mặc định. Tìm phần Stars (trên đầu). Bạn chọn Sao màu theo mặc định của Google hoặc chọn nhiều màu theo ý thích.

Ngoài ra, bạn có thể kéo-và-thả mỗi ngôi sao hay biểu tượng đến phần In use: category từ mục Not in use. Với cách làm này bạn sẽ chọn được số lượng sao màu như ý muốn để sau này sử dụng.

Khi đã xong, bạn kéo xuống đáy của màn hình cài đặt và nhấp chuột lưu thay đổi Save Changes. Sau đó, nó sẽ dẫn bạn trở lại hộp thư đến Inbox.

Khi muốn đánh dấu vào bức email nào, hãy thêm màu cho ngôi sao bằng cách nhấp vào ngôi sao 1 lần, mặc định là màu vàng. Nhấp chuột thêm lần nữa sẽ hiển thị màu tiếp theo khác cho ngôi sao đó. Cứ thế nhấp chuột liên tiếp thì bạn sẽ thấy sự thay đổi màu sắc của ngôi sao, và dừng ở màu sắc mà bạn muốn dùng để đánh dấu.

=> Đánh dấu và phân loại email bằng cách sử dụng màu sắc của biểu tượng đánh dấu hình ngôi sao giúp cho bạn rèn luyện trí nhớ tốt hơn cũng như là cách sắp xếp công việc thuận tiện, nhanh hơn.