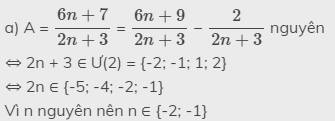Giúp mình với tìm số nguyên n để A=6n+7 phần 2n+3 nguyên

Những câu hỏi liên quan
1/TÌM X
2/3-1/3.(X-3/2)-1/2:(2X+1)=5
2/CHO P/S B=6n+7/2n+3
a)Tìm số nguyên n để B có giá trị nguyên
làm nhanh giúp mình, mình đag cần gấp
a) A = \(\dfrac{6n+7}{2n+3}\) = \(\dfrac{6n+9}{2n+3}\) − \(\dfrac{2}{2n+3}\) nguyên
⇔ 2n + 3 ∈ Ư(2) = {-2; -1; 1; 2}
⇔ 2n ∈ {-5; -4; -2; -1}
Vì n nguyên nên n ∈ {-2; -1}
Đúng 1
Bình luận (0)
Bài 2:
a) Để B nguyên thì \(6n+7⋮2n+3\)
\(\Leftrightarrow-2⋮2n+3\)
\(\Leftrightarrow2n+3\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow2n\in\left\{-2;-4\right\}\)
hay \(n\in\left\{-1;-2\right\}\)
Đúng 1
Bình luận (0)
tìm số nguyên n để :
a) (6n-4) chia hết cho (1-2n)
b) (3-2n) chia hết cho (3n+1)
giúp mình với nha!Mình đang gấp.
a)(6n-4) chia hết cho (1-2n)
Ta có (1-2n)=3(1-2n)=3-6n
\(\Rightarrow\)(6n-4+3-6n)\(⋮\)(1-2n)
\(\Rightarrow\)(-1)\(⋮\)(1-2n)\(\Rightarrow\)(1-2n)\(\in\) Ư(1)={±1}
Ta có bảng
| 1-2n | -1 | 1 |
| 2n | 2 | 0 |
| n | 1 | 0 |
Vậy...
T.i.c.k cho mình nhé
#TMCho phân số \(A=\frac{6n+7}{2n+3}\)
a) Tìm số nguyên n để A có giá trị nguyên.
b) Tìm số nguyên n để a có giá trị nhỏ nhất.
a) \(A=\frac{6n+7}{2n+3}=\frac{6n+9}{2n+3}-\frac{2}{2n+3}\) nguyên
<=> 2n + 3 thuộc Ư(2) = {-2; -1; 1; 2}
<=> 2n thuộc {-5; -4; -2; -1}
Vì n nguyên nên n thuộc {-2; -1}
b) A có GTNN <=> \(\frac{2}{2n+3}\) có GTLN
<=> 2n + 3 là số nguyên dương nhỏ nhất
<=> 2n + 3 = 1
<=> 2n = -2
<=> n = -1
Đúng 0
Bình luận (0)
a)\(A=\frac{6n+7}{2n+3}=\frac{2n+2n+2n+3+4}{2n+3}=\frac{4}{2n+3}\)
\(\Rightarrow2n+3\in\text{Ư}\left(4\right)=\left\{1;2;4;-1;-2;-4\right\}\)
Nếu 2n+3 = 1 => n = -2 (nhận)
Nếu 2n+3 = 2 => n =-0,5 (loại)
Nếu 2n + 3 = 4 => n = 3,5 (loại)
Nếu 2n + 3 = -1 => n = 1 (nhận)
Nếu 2n + 3 = -2 => n = -2,5 (loại)
Nếu 2n + 3 = -4 => n =-3,5 (loại)
Vậy n \(\in\) {-2;1}
b) A GTNN => \(\frac{2}{2n+3}\) có GTLN
=> 2n + 3 là số nguyên dương nhỏ nhất
=> 2n + 3 = 1
=> 2n = -2
=> n = -1
Đúng 0
Bình luận (2)
Tìm tất cả các số nguyên n sao cho số A = \(\frac{1-6n}{2n-3}\)là một số nguyên.
(Đề thi lớp 7 trường AMSTERDAM)
Giúp mình nha
\(A=\frac{1-6n}{2n-3}=\frac{-6n+9-8}{2n-3}=-3+\frac{-8}{2n-3}\)
Để \(A\in Z\Rightarrow\frac{-8}{2n-3}\in Z\)
\(\Rightarrow-8⋮2n+3\)
\(\Rightarrow2n+3\inƯ\left(-8\right)\)
\(\Rightarrow2n+3\in\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
Vì \(2n+3\)là số lẻ
\(\Rightarrow2n+3\in\left\{1;-1\right\}\)
\(\Rightarrow2n\in\left\{-2;-4\right\}\)
\(\Rightarrow n\in\left\{-1;-2\right\}\)
Vậy...
A=\(\frac{1-6n}{2n-3}\)
=\(\frac{-6n+9-8}{2n-3}\)
= \(-3+\frac{-8}{2n-3}\)
để \(A\inℤ\Leftrightarrow\frac{-8}{2n-3}\inℤ\)
\(\Leftrightarrow-8⋮2n+3\)
\(\Leftrightarrow2n+3\inƯ\left(-8\right)\)
MÀ Ư(-8)=\(\hept{\pm1;\pm2;\pm4;\pm8}\)
VÌ 2n+3 là số lẻ nên ta có bảng:
| 2n+3 | 1 | -1 |
| 2n | -2 | -4 |
| n | -1 | -2 |
vậy n\(\in\hept{-1;-2}\)
thì A là 1 số nguyên
Cảm ơn bạn Phương nha!
cho n thuộc số tự nhiên .Chứng minh :
a , 6n+7 và 2n+2 là 2 số nguyên tố cùng nhau
b. 6n+7 và 2n+1 là nguyên tố cùng nhau
CÁC BẠN GIẢI BÀI TẬP NÀY GIÚP MÌNH VỚI ...THANK YOU CÁC BẠN YÊU !!!
cho phân số B=\(\frac{6n+7}{2n+3}\)
a) tìm số nguyên n để B có giá trị nguyên.
b) tìm số nguyên n để B có giá trị nhỏ nhất.
Tìm gtri nguyên của n để A chia hết cho B
A=n3+6n2-4, B= 2n -1
Giải giúp mình với mình cần gấp ahuhuhu TT---TT
1.Chứng minh rằng với n thuộc tập hợp số tự nhiên khác 0 , các phân số sau là các phân số tối giản :
a) 3n-2/4n-3
b) 4n+1/6n+1
2.Cho B=n/n-4
Tìm n thuộc tập hợp các số nguyên để B có giá trị nguyên
3.Cho C=2n+7/n+3
Tìm n thuộc tập hợp các số nguyên để C có giá trị nguyên
Lưu ý : Các bạn giải giúp mình ghi rõ cách giải ra nhé
tìm n là số nguyên để 2n-1/2n+3 là số nguyên , ai giúp mình với.
Ta có:
\(\dfrac{2n-1}{2n+3}=\dfrac{2n+3-4}{2n+3}\)\(=1-\dfrac{4}{2n+3}\)
Để \(\dfrac{2n-1}{2n+3}\) là số nguyên thì \(2n+3\inƯ\left(4\right)\)
Ta có bảng:
| \(2n+3\) | \(-4\) | \(-2\) | \(-1\) | \(1\) | \(2\) | \(4\) |
| \(2n\) | \(-7\) | \(-5\) | \(-4\) | \(-2\) | \(-1\) | \(1\) |
| \(n\) | \(-\dfrac{7}{2}\left(loại\right)\) | \(-\dfrac{5}{2}\left(loại\right)\) | \(-2\) | \(-1\) | \(-\dfrac{1}{2}\left(loại\right)\) | \(\dfrac{1}{2}\left(loại\right)\) |
Vậy \(n\in\left\{-2;-1\right\}\)
Đúng 1
Bình luận (0)
Để A nguyên thì 2n-1 chia hết cho 2n+3
=>2n+3-4 chia hết cho 2n+3
=>\(2n+3\in\left\{1;-1;2;-2;4;-4\right\}\)
mà n nguyên
nên \(n\in\left\{-1;-2\right\}\)
Đúng 1
Bình luận (0)