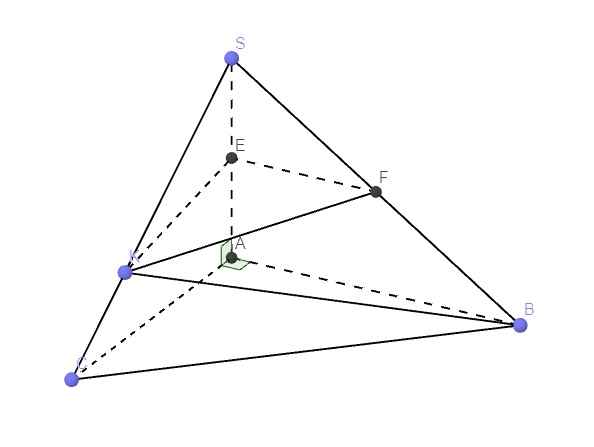
Giúp mình câu 21 phần b với ạ

Những câu hỏi liên quan
Ai giúp mình câu b phần 2 bài III với cả câu b bài IV với ạ. Mình xin cảm ơn rất rất nhiều ạ.

Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
Đúng 3
Bình luận (0)
Bài IV.b.
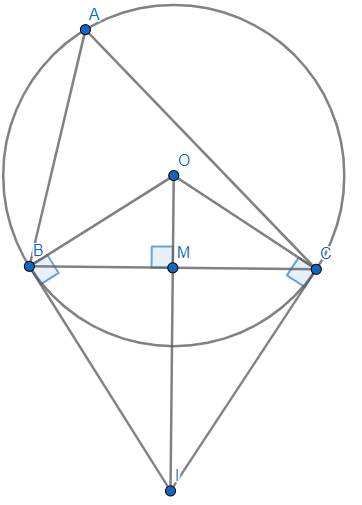
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
Đúng 2
Bình luận (0)
Câu 21 với 22 giúp mình với ạ 
21.
\(\left\{{}\begin{matrix}SA\perp AB\\AC\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAC\right)\)
E là trung điểm SA, F là trung điểm SB \(\Rightarrow\) EF là đường trung bình tam giác SAB
\(\Rightarrow EF||AB\Rightarrow EF\perp\left(SAC\right)\)
\(\Rightarrow EF=d\left(F;\left(SEK\right)\right)\)
\(SE=\dfrac{1}{2}SA=\dfrac{3a}{2}\) ; \(EF=\dfrac{1}{2}AB=a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{13}\Rightarrow SK=\dfrac{2}{3}SC=\dfrac{2a\sqrt{13}}{3}\)
\(\Rightarrow S_{SEK}=\dfrac{1}{2}SE.SK.sin\widehat{ASC}=\dfrac{1}{2}.\dfrac{3a}{2}.\dfrac{2a\sqrt{13}}{3}.\dfrac{2a}{a\sqrt{13}}=a^2\)
\(\Rightarrow V_{S.EFK}=\dfrac{1}{3}EF.S_{SEK}=\dfrac{1}{3}.a.a^2=\dfrac{a^3}{3}\)
\(AB\perp\left(SAC\right)\Rightarrow AB\perp\left(SEK\right)\Rightarrow AB=d\left(B;\left(SEK\right)\right)\)
\(\Rightarrow V_{S.EBK}=\dfrac{1}{3}AB.S_{SEK}=\dfrac{1}{3}.2a.a^2=\dfrac{2a^3}{3}\)
Đúng 1
Bình luận (0)
22.
Gọi D là trung điểm AB
Do tam giác ABC đều \(\Rightarrow CD\perp AB\Rightarrow CD\perp\left(SAB\right)\)
\(\Rightarrow CD=d\left(C;\left(SAB\right)\right)\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
N là trung điểm SC \(\Rightarrow d\left(N;\left(SAB\right)\right)=\dfrac{1}{2}d\left(C;\left(SAB\right)\right)=\dfrac{a\sqrt{3}}{2}\)
\(S_{SAB}=\dfrac{1}{2}SA.AB=a^2\sqrt{3}\) \(\Rightarrow S_{SAM}=\dfrac{1}{2}S_{SAB}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{SAMN}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3}{4}\)
Lại có:
\(V_{SABC}=\dfrac{1}{3}SA.S_{ABC}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}=a^3\)
\(\Rightarrow V_{A.BCMN}=V_{SABC}-V_{SANM}=\dfrac{3a^3}{4}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình phần câu b,c với ạ mình cần gấp 




Giúp mình câu 7 phần b với ạ!
giúp mình với ạ
-1/21 - 1/28 =
/ nghĩa là phần
\(-\dfrac{1}{21}-\dfrac{1}{28}\)
\(=-\dfrac{28}{588}-\dfrac{21}{588}\)
\(=-\dfrac{49}{588}=-\dfrac{1}{12}\)
Đúng 1
Bình luận (1)
-1/21 - 1/28
=-28/588 - 21/588
= -1/12
lấy máy tính là dc mà
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Giải giúp mình câu 20 và 21 với ạ
20.
Ta có:
$2p + n = 49$
$n = .2p53,125\%$
Suy ra : $p = 16 ; n = 17$
Vậy nguyên tử có 16 hạt proton, 16 hạt electron, 17 hạt notron
A là nguyên tố Lưu huỳnh, kí hiệu : S
Số khối : A = p + n = 33
21.
Ta có :
$2p + n = 46$
$2p : n = 15 : 8$
Suy ra p = 15 ; n = 16
Vậy nguyên tử có 15 hạt proton, 15 hạt electron và 16 hạt notron
Số khối = p + n = 31
Kí hiệu A : P(photpho)
Đúng 1
Bình luận (0)
Bài 20:
Vì tổng số hạt cơ bản của nguyên tố A là 49: S=2P+ N=40 (1)
Mặt khác, số hạt không mang điện chiếm 53,125% số hạt mang điện: N=53,125%.2P= 106,25%P (2)
Từ (1), (2) ta lập được hệ pt:
\(\left\{{}\begin{matrix}2P+N=49\\N=106,25\%P\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}P=E=Z=16\\N=17\end{matrix}\right.\)
=> Nguyên tử này có 16e, 16p, 17n.
Số khối: A=P+N=16+17=33(đ.v.C)
KH đầy đủ A: \(^{33}_{16}S\)
Đúng 0
Bình luận (0)
GIÚP MÌNH ĐIỀN TỪ CÂU 15 --> 21 VỚI Ạ!!
15.had never seen-visited
16.am doing
17.am reading
18.am still waiting
19.are they speaking
20.is stealing
21.was working-was shopping
Đúng 1
Bình luận (0)
 GIÚP MÌNH TỪ CÂU 21 ĐẾN 30 VỚI Ạ
GIÚP MÌNH TỪ CÂU 21 ĐẾN 30 VỚI Ạ
21 which
defining
22 which
defining
23 which
defining
24 who
non-defining
25 that
defining
26 whose
defining
27 who
non-defining
28 that
defining
29 which
non-defining
30 whose
defining
Đúng 5
Bình luận (0)
mọi người ơi, giúp mình câu 21 với ạ. Cảm mơn ^^