Cho hình vuông ABCD có cạnh là 1 mét. Trên các cạnh hình vuông lấy các trung điểm, nối các trung điểm thì lại được hình vuông mới. Tiếp tục nối trung điểm của hình vuông mới này ta lại được hình vuông mới nhỏ hơn. Cứ làm như vậy vô hạn lần.

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh là 1 mét. Trên các cạnh hình vuông lấy các trung điểm, nối các trung điểm thì lại được hình vuông mới. Tiếp tục nối trung điểm của hình vuông mới này ta lại được hình vuông mới nhỏ hơn. Cứ làm như vậy vô hạn lần.
Cách giải luôn nhé !
bài đó trog toán vui tuần này chứ zì
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh là 1 mét. Trên các cạnh hình vuông lấy các trung điểm, nối các trung điểm thì lại được hình vuông mới. Tiếp tục nối trung điểm của hình vuông mới này ta lại được hình vuông mới nhỏ hơn. Cứ làm như vậy vô hạn lần. Hãy tính tổng diện tích tất cả các hình vuông đó?
Gọi diện tích hình vuông lớn nhất là 1. Thì tổng diện tích sẽ là:
1 + 1/2 + 1/4 + 1/8 + 1/16 + ….. + 1/n =
Nhân với 2 ta được:
2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + ….. + 1/(n :2) =
Tổng diện tích là: (Trừ đi biểu thức ban đầu)
2 – (1 + 1/2 + 1/4 + 1/8 + 1/16 + ….. + 1/n:2+ 1/n) = 2 – 1/n
n càng lớn thì 1/n càng bé (không đáng kể).
Tổng diện tích gấp 2 lần diện tích ban đầu.
Tổng diện tích là:
1 x 1 x 2 = 2 (m2)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh là 1 mét. Trên các cạnh hình vuông lấy các trung điểm, nối các trung điểm thì lại được hình vuông mới. Tiếp tục nối trung điểm của hình vuông mới này ta lại được hình vuông mới nhỏ hơn. Cứ làm như vậy vô hạn lần.
Hãy tính tổng diện tích tất cả các hình vuông đó?
Cho hình vuông ABCD có cạnh là 1 mét. Trên các cạnh hình vuông lấy các trung điểm, nối các trung điểm thì lại được hình vuông mới. Tiếp tục nối trung điểm của hình vuông mới này ta lại được hình vuông mới nhỏ hơn. Cứ làm như vậy vô hạn lần.
ABCD
Hãy tính tổng diện tích tất cả các hình vuông đó
Bài toán 47
Cho hình vuông ABCD có cạnh là 1 mét. Trên các cạnh hình vuông lấy các trung điểm, nối các trung điểm thì lại được hình vuông mới. Tiếp tục nối trung điểm của hình vuông mới này ta lại được hình vuông mới nhỏ hơn. Cứ làm như vậy vô hạn lần.Hãy tính tổng diện tích tất cả các hình vuông đó?
Gọi diện tích hình vuông lớn nhất là 1. Thì tổng diện tích sẽ là:
1 + 1/2 + 1/4 + 1/8 + 1/16 + ….. + 1/n =
Nhân với 2 ta được:
2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + ….. + 1/(n :2) =
Tổng diện tích là: (Trừ đi biểu thức ban đầu)
2 – (1 + 1/2 + 1/4 + 1/8 + 1/16 + ….. + 1/n:2+ 1/n) = 2 – 1/n
n càng lớn thì 1/n càng bé (không đáng kể).
Tổng diện tích gấp 2 lần diện tích ban đầu.
Tổng diện tích là:
1 x 1 x 2 = 2 (m2)
Đúng 0
Bình luận (0)
Cho hình vuông có cạnh là 4m.Trên mỗi cạnh hình vuông lấy trung điểm của nó nối các trung điểm này ta được hình vuông mới.Tính diện tích hình vuông mới?
Diện tích hình vuông lớn là:
4 x 4 = 16 (m2)
Diện tích hình vuông mới là:
16 : 2 = 8 (cm2)
Đáp số: 8 cm2
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh 16 cm.Lấy trung điểm của các cạnh rồi nối lại ta được hình vuông thứ 2, rồi tiếp tục làm như vậy cho đến khi có hình vuông cạnh 4 cm
Cho hình vuông abcd có cạnh dài 256cm. Lấy trung điểm của các cạnh rồi nối lại ta được hình vuông thứ hai, rồi cứ tiếp tục làm như vậy cho đến hình vuông thứ 15.
a) Tính độ dài cạnh hình vuông thứ 15.
b)Tổng chu vi của tất cả các hình vuông có số thứ tự lẻ trong 15 hình vuông nói trên là bao nhiêu cm.
Độ dài cạnh hình vuông thứ 15 :
\(256:\left(\left(15+1\right)x8\right)=2\left(cm\right)\)
b) Chu vi hình vuông thứ 15 :
\(2x4=8\left(cm\right)\)
Chu vi hình vuông thứ 13 :
\(4x4=64\left(cm\right)\)
Chu vi hình vuông thứ 11 :
\(8x4=32\left(cm\right)\)
Chu vi hình vuông thứ 9 :
\(16x4=64\left(cm\right)\)
Chu vi hình vuông thứ 7 :
\(32x4=128\left(cm\right)\)
Chu vi hình vuông thứ 5 :
\(64x4=256\left(cm\right)\)
Chu vi hình vuông thứ 3 :
\(128x4=512\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho một hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được một hình vuông, tiếp tục làm như thế đối với hình vuông mới (như hình vẽ bên). Tổng diện tích cách hình vuông liên tiếp đó là A. 2 B.
3
2
C. 8 D. 4
Đọc tiếp
Cho một hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được một hình vuông, tiếp tục làm như thế đối với hình vuông mới (như hình vẽ bên).
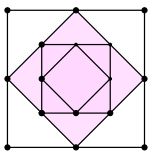
Tổng diện tích cách hình vuông liên tiếp đó là
A. 2
B. 3 2
C. 8
D. 4
Đáp án A
Theo giả thiết, diện tích hình vuông sau sẽ bằng 1 2 diện tích hình vuông trước.
Khi đó, tổng diện tích cần tính là tổng của cấp số nhân với u 1 = 1 , , với công bội q = 1 2 .
Vậy tổng S = u 1 1 − q n 1 − q = 1 1 − 2 − n 1 − 1 2
mà n → + ∞ ⇒ 2 − n → 0 suy ra S=2
Đúng 0
Bình luận (0)

















