Cho tam giác ABC có góc A tù. D là điểm nằm giữa A, B. E là điểm nằm giữa A và C. Chứng minh rằng
BC > DE.

Những câu hỏi liên quan
Cho tam giác ABC có \(\widehat {BAC}\) là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
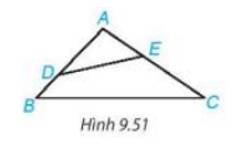
Ta có \(\widehat {BAC}\) là góc tù nên \(\widehat {ADE},\widehat {AED}\) là các góc nhọn
\( \Rightarrow \widehat {DEC}\) là góc tù
\( \Rightarrow DE < DC\) (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat {DAC}\) là góc tù nên \(\widehat {ADC},\widehat {ACD}\) là các góc nhọn
\( \Rightarrow \widehat {BDC}\) là góc tù.
\( \Rightarrow DC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE
Đúng 0
Bình luận (0)
Cho tam giác ABC có ˆBAC���^ là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE BC.
Đọc tiếp
Cho tam giác ABC có là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
góc CAD>90 độ
=>góc CED>90 độ
=>ED<CD
goc CDB=góc DAC+góc ACD
=>góc CDB>90 độ
=>CD<BC
=>ED<BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A tù, điểm D nằm giữa A và B, điểm E nằm giữa A và C. Chứng minh BC > DE
Bạn tham khảo ở đây nhé!!
https://h.vn/hoi-dap/question/269901.html
hok tốt!!
~
Vì góc bac là góc tú nên độ dài ab lớn
Mà d nằm giữa ba và e năm giữa ac nên
De<bc
1) Cho góc xAy = 90 độ. Trên cạnh Ax lấy hai điểm B và D ( D nằm giữa A và B ) , trên cạnh Ay lấy hai điểm C và E ( C nằm giữa A và E ) sao cho AD = AC ; AB = AE
a) Chứng minh : tam giác ABC = tam giác AED ; tam giác BCE = tam giác EDB
b) Đường thẳng qua A vuông góc với BC tại H và cắt DE tại M. Chứng minh M là trung điểm của DE
Cho tam giác cân tại A. ( góc A là góc tù) trên cạnh BC lấy điểm E sao cho BE= CD điểm E nằm giữa hai điểm B và D. Kẻ trung tuyến AM của tam giác ABC chứng minh EH, DK,AM cùng đi qua một điểm
Giải thích các bước giải:
a)Xét tam giác BAD và tam giác BED:
BD:cạnh chung
^ABD=^EBD (vì BD là tia phân giác của ^ABC)
AB=BE(gt)
=>tam giác BAD=tam giác BED(c.g.c)
b)Từ tam giác BAD=tam giác BED(cmt)
=>AD=DE(cặp cạnh t.ứ)
và ^BAD=^BED(cặp góc .tứ),mà ^BAD=900 (^BAC=900)=>^BED=900
Xét tam giác DFA vuông ở A và tam giác DCE vuông ở E có:
AD=AE (cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác DFA=tam giác DCE(cgv-gnk)
=>DF=DC(cặp cạnh t.ứ)
=>tam giác DFC cân tại D (dấu hiệu nhận biết tam giác cân)
c)Từ tam giác DFA=tam giác DCE (cmt)
=>AF=CE(cặp cạnh t.ứ)
Ta có: BE+CE=BC
BA+AF=BF
mà AF=CE(cmt),AB=AE(gt)
=>BC=BF
=>tam giác BFC cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BCF=1800−FBC21800−FBC2 (tính chất tam giác cân) (1)
Vì AB=AE(gt)
=>tam giác ABE cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BEA=1800−ABE21800−ABE2 (tính chất tam giác cân) (2)
Từ (1);(2);lại có ^ABE=^FBC
=>^BCF=^BEA,mà 2 góc này nằm ở vị trí đồng vị
=>AE//CF(dấu hiệu nhận biết 2 đg thẳng song song)
Cho tam giác vuông ABC có A=90°. D là một điểm nằm giữa A và B . E là một điểm nằm giữa A và C. nối B với E , D với E .chứng minh :
a, BE < BC.
b, DE < BC
Cho ABC (AB < AC). Gọi D là điểm nằm giữa A và B, E là điểm nằm giữa A và C và BD = CE. Gọi M, N, I lần lượt là trung điểm của BC, DE, BE.. a)Đường thẳng MN cắt đường thẳng AB ởP, cắt đường thẳng AC ởQ. Chứng minh tam giác APQ cân.b )Kẻphân giác AF của tam giác ABC. Chứng minh MN // AF.
cho tam giác ABC có A=120 độ . Trên tia phân giác của góc A lấy hai điểm D và E ( D nằm giữa A và E ) sao cho AB = AD , DE=AC . Chứng minh rằng tam giác BCE là tam giác đều
Cho tam giác ABC có góc A tù. Vẽ AD vuông góc AB và AD=AB (tia AD nằm giữa hai tia AB và AC), AE vuông góc AC và AE=AC (tia AE nằm giữa hai tia AB và AC). Gọi M là trung điểm của BC. Chứng minh rằng: AM vuông góc DE
















