cho nửa đường tròn tâm O đường kính AB.C là 1 điểm bất kì thuộc nửa đường tròn.kẻ CD vuông góc với AB.Trên OC lấy E sao cho OE=CD.tìm quỹ tích điểm E

Những câu hỏi liên quan
Cho nửa đường tròn tâm O bán kính CD. Từ C,D kẻ các tiếp tuyến Cx,Dy với nửa đường tròn tâm O.
Trên nửa đường tròn lấy điểm E, điểm M bất kì nằm trên CD(M khác C,D,O).Qua E kẻ đường thẳng vuông góc với EM và cắt Cx,Dy tại A,B.C/m góc AMB =90o
Cho nửa đường tròn tâm O đường kính AB C là 1 điểm thuộc nửa đường tròn H là hình chiếu của C trên AB . Qua trung điểm M của CH kẻ đường vuông góc với OC cắt nửa đường tròn tại D và E . CMR AB là tiếp tuyến đường tròn tâm C bán kính CD
Tôi cũng có bài khó giống ý hệt bạn,vậy bạn có hướng làm chưa
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm o đường kính ab trên nửa đường tròn lấy điểm c sao cho ca <cb,vẽ ch vuông góc với ab (h thuộc ab).trên cung bc lấy điểm d bất kì (d khác b và c),gọi e là giao diểm của ch và ad.
a)chứng minh tứ giác bdhe nội tiếp đường tròn
b)chứng minh ac bình phương = ae.ad
a: góc EHB+góc EDB=180 độ
=>BDHE nội tiếp
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC^2=AE*AD
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O,đường khính AB.Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn đối với AB.Vẽ bán kính OE bất kì,tiếp tuyến của nửa mặt đường tròn tại E cắt Ax,By lần lượt ở Ca)CMR: CDAC+BDb)Tính số đo góc CODc) Gọi M là giao điểm của OC và AE;N là giao điểm của OD và BE.Tứ giác MENO là hình gì?Vì sao?d)Gọi R là độ dài bán kính của đường tròn tâm O.Tính AC.DB
Đọc tiếp
Cho nửa đường tròn tâm O,đường khính AB.Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn đối với AB.Vẽ bán kính OE bất kì,tiếp tuyến của nửa mặt đường tròn tại E cắt Ax,By lần lượt ở C
a)CMR: CD=AC+BD
b)Tính số đo góc COD
c) Gọi M là giao điểm của OC và AE;N là giao điểm của OD và BE.Tứ giác MENO là hình gì?Vì sao?
d)Gọi R là độ dài bán kính của đường tròn tâm O.Tính AC.DB
Cho đường tròn tâm O đường kính AB; trên nửa đường tròn lấy điểm C sao cho AC>AB, qua C dựng đường thẳng vuông góc với OC cắt đường thẳng AB tại D. Kẻ CH vuông góc với AB (H thuộc AB), kẻ BK vuông góc với CD ( K thuộc CD); đường kính CH cắt đường thẳng BK tại E. a) Chứng minh 4 điểm C,H,B,K cùng thuộc 1 đường tròn. b) Cm KH//AC. c) Cm BH.AD=AH.BD
a: Ta có: \(\widehat{CHB}=90^0\)
=>ΔCHB vuông tại H
=>ΔCHB nội tiếp đường tròn đường kính CB(4)
Ta có: \(\widehat{CKB}=90^0\)
=>ΔCKB vuông tại K
=>ΔCKB nội tiếp đường tròn đường kính CB(5)
Từ (4) và (5) suy ra C,H,B,K cùng thuộc đường tròn đường kính CB
b:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: \(\widehat{OCB}+\widehat{BCK}=\widehat{OCK}=90^0\)
\(\widehat{OCB}+\widehat{OCA}=\widehat{BCA}=90^0\)
Do đó: \(\widehat{BCK}=\widehat{OCA}\)(1)
Ta có: CHBK là tứ giác nội tiếp
=>\(\widehat{BCK}=\widehat{BHK}\left(2\right)\)
Xét ΔOAC có OC=OA
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)(3)
Từ (1),(2),(3) suy ra \(\widehat{BHK}=\widehat{OAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//AC
Đúng 1
Bình luận (0)
vẽ hộ hình giúp mình với phần a) Cm 2 tam giác nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB; trên nửa đường tròn lấy điểm C sao cho AC>AB, qua C dựng đường thẳng vuông góc với OC cắt đường thẳng AB tại D. Kẻ CH vuông góc với AB (H thuộc AB), kẻ BK vuông góc với CD ( K thuộc CD); đường kính CH cắt đường thẳng BK tại E. Chứng mình 4 điểm C,H,B,K cùng thuộc 1 đường tròn'
Xét tứ giác CHBK có
\(\widehat{CHB}+\widehat{CKB}=90^0+90^0=180^0\)
=>CHBK là tứ giác nội tiếp
=>C,H,B,K cùng thuộc một đường tròn
Đúng 0
Bình luận (1)
Cho nửa đường tròn tâm O đường kính AB. Lấy điểm H cố định trên đoạn OA, đường vuông góc với OA tại H cắt nửa đường tròn tại C. Gọi N là trung điểm của BC. M là điểm bất kì thuộc cung nhỏ BC (M ≠ B; M ≠ C). Tia BM cắt HC tại K; AM cắt HC tại E. Chứng minh rằng tâm I của đường tròn ngoại tiếp tam giác AEK di chuyển trên một đường thẳng cố định khi M di chuyển trên cung nhỏ BC.
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Lấy điểm H cố định trên đoạn OA, đường vuông góc với OA tại H cắt nửa đường tròn tại C. Gọi N là trung điểm của BC. M là điểm bất kì thuộc cung nhỏ BC (M ≠ B; M ≠ C). Tia BM cắt HC tại K; AM cắt HC tại E. Chứng minh rằng tâm I của đường tròn ngoại tiếp tam giác AEK di chuyển trên một đường thẳng cố định khi M di chuyển trên cung nhỏ BC.
AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm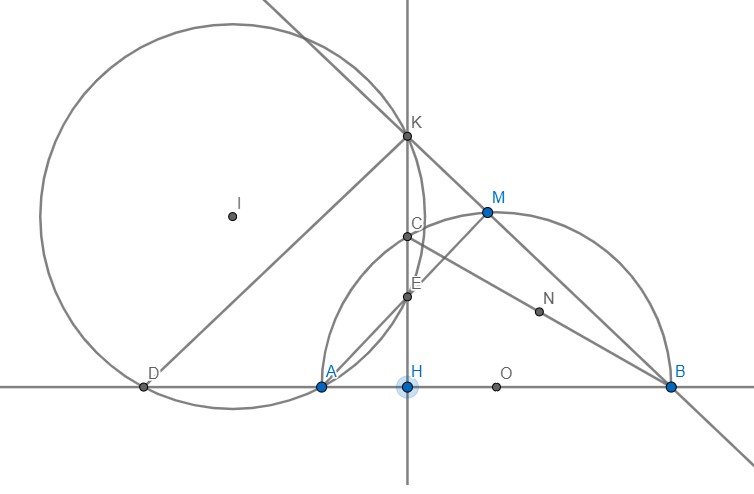
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O,đường kính AB.Gọi Ax,By là các tia vuông góc với AB.Qua điểm E thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn cắt Ax và By lần lượt tại C và D
a)Chứng minh CD=AC+BD
b)Gọi I là giao điểm của OC và AE,gọi K là giao điểm của OD và BE.Tứ giác EIOK là hình gì?Vì sao?
a: Xet (O) có
CE,CA là các tiếp tuyến
nên CE=CA và OC là phân giác của góc EOA(1)
mà OE=OA
nên OC là trung trực của AE
=>OC vuông góc với AE
Xét (O) có
DE,DB là các tiếp tuyến
nen DE=DB và OD là phân giác của góc EOB(2)
mà OE=OB
nên OD là trung trực của BE
=>OD vuông góc với BE
CE+ED=CD
=>CD=CA+BD
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
Xét tứ giác EIOK co
góc EIO=góc EKO=góc IOK=90 độ
nên EIOK là hình chữ nhật
Đúng 1
Bình luận (0)
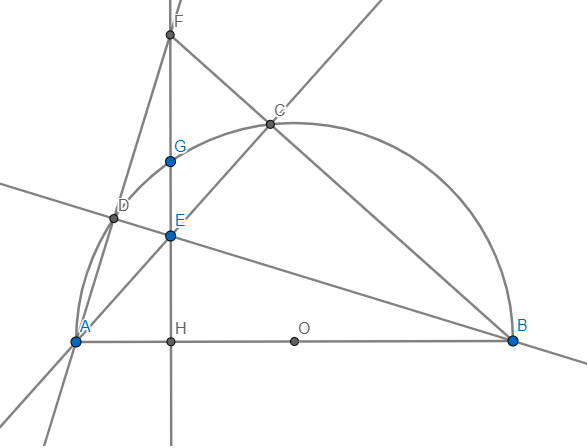
Cho nửa đường tròn (O),đường kính AB.Trên nửa đường tròn (O) lấy điểm G tùy ý (G khác A và B).Vẽ GH vuông góc với AB (H thuộc AB);trên đoạn thẳng HG lấy một điểm E (E khác H và G).Các tia AE và BE cắt nửa đường tròn (O) lần lượt tại C và D.Gọi F là giao điểm của hai tia BC và AD.Chứng minh rằng :a)Tứ giác ECFD nội tiếp được trong một đường trònb)Bốn điểm H,E,G,F thẳng hàng
Đọc tiếp
Cho nửa đường tròn (O),đường kính AB.Trên nửa đường tròn (O) lấy điểm G tùy ý (G khác A và B).Vẽ GH vuông góc với AB (H thuộc AB);trên đoạn thẳng HG lấy một điểm E (E khác H và G).Các tia AE và BE cắt nửa đường tròn (O) lần lượt tại C và D.Gọi F là giao điểm của hai tia BC và AD.Chứng minh rằng :
a)Tứ giác ECFD nội tiếp được trong một đường tròn
b)Bốn điểm H,E,G,F thẳng hàng
a) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle ACB=90\)
\(\Rightarrow\angle FDE+\angle FCE=90+90=180\Rightarrow ECFD\) nội tiếp
b) GH cắt AD tại F'.F'B cắt AE tại C'
Ta có: \(\left\{{}\begin{matrix}F'H\bot AB\\BD\bot AF'\end{matrix}\right.\Rightarrow E\) là trực tâm \(\Delta F'AB\Rightarrow AE\bot F'B\Rightarrow AC'\bot F'B\)
mà AB là đường kính \(\Rightarrow C'\in\left(O\right)\Rightarrow C\equiv C'\Rightarrow F'\equiv F\Rightarrow\) đpcm
Đúng 2
Bình luận (0)















