CMR trong 1 tứ giác thì tổng các góc ngoài tại mỗi đỉnh bằng 3600
Cmr trong 1 tứ giác tổng hai góc ngoài tại 2 đỉnh bằng tổng 2 góc trong tại các đỉnh còn lại?
Cho tứ giác ABCD. CMR tổng 2 góc ngoài tại đỉnh A và C bằng tổng 2 góc trong tại đỉnh B và D
Xét tứ giác ABCD có:
\(\widehat{A_2}+\widehat{B_2}+\widehat{C_1}+\widehat{D_1}=360^0\left(...\right)\)
Mà \(\widehat{A_1}+\widehat{A_2}=180^0\left(KB\right),\widehat{C_1}+\widehat{C_2}=180^0\left(KB\right)\Rightarrow\widehat{A_1}+\widehat{A_2}+\widehat{C_1}+\widehat{C_2}=360^0\)
\(\Rightarrow\widehat{A_1}+\widehat{C_2}=\widehat{B_2}+\widehat{D_1}\)
Vậy ...
Chứng minh rằng trong 1 tứ giác tổng góc ngoài tại 2 đỉnh bằng tổng hai góc trong tại các đỉnh còn lại
Ta có góc B2 = 180 độ - góc B1
góc C2 = 180 độ - góc C1
=> góc B2 + góc C2 = 360 độ - ( góc B1 + góc C1 ) (1)
Tứ giác ABCD có góc A + góc B + góc C + góc D = 360 độ
=> góc A + góc D = 360 độ - ( góc B1 + góc C1 ) (2)
Từ (1), (2) => góc B2 + góc C2 = góc A + góc D
Vậy tổng 2 góc ngoài tại 2 đỉnh bằng tổng 2 góc trong tại các đỉnh còn lại
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là
A. 3000
B. 2700
C. 1800
D. 3600
1, chứng minh rằng các góc của 1 tứ giác không thể đều là góc nhọn, không thể đều là góc tù
2, cho tứ giác ABCD chứng minh rằng tổng 2 góc ngoài tại đỉnh A vàC bằng tổng hai góc trong tại các đỉnh B và C
1 ta có :1 tứ giác có 4 góc và tổng phải bằng 360 độ mà 4 góc nhọn sẽ bé hơn 360(vì 1 góc nhọn <90 độ ) nên cac góc ko thể đều là góc nhọn.Đối với góc tù vẫn tương tự
Cho tứ giác ABCD. Chứng minh rằng tổng hai góc ngoài tại các đỉnh A và C bằng tổng hai góc trong tại các đỉnh B và D.
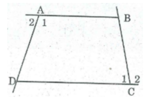
* Gọi ∠ A 1 , ∠ C 1 là góc trong của tứ giác tại đỉnh A và C, ∠ A 2 , ∠ C 2 là góc ngoài tại đỉnh A và C.
Ta có: ∠ A 1 + ∠ A 2 = 180 0 (2 góc kề bù)
⇒ ∠ A 2 = 180 0 - ∠ A 1
∠ C 1 + ∠ C 2 = 180 0 (2 góc kề bù) ⇒ ∠ C 2 = 180 0 - ∠ C 1
Suy ra: ∠ A 2 + ∠ C 2 = 180 0 - ∠ A 1 + 180o - ∠ C 1 = 360 0 – ( ∠ A 1 + ∠ C 1 ) (1)
* Trong tứ giác ABCD ta có:
∠ A 1 + ∠ B + ∠ C 1 + ∠ D = 360 0 (tổng các góc của tứ giác)
⇒ ∠ B + ∠ D = 360 0 - ( ∠ A 1 + ∠ C 1 ) (2)
Từ (1) và (2) suy ra: ∠ A 2 + ∠ C 2 = ∠ B + ∠ D
Tính tổng các góc ngoài của tứ giác ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).
4 góc tứ giác là a,b,c,d
=.4 góc ngoài =180-a,180-b,180-c,180-d
=>tổng chúng =720độ - 360 độ=360 độ
Gọi 4 góc của tứ giác là : a , b , c , d
Thì 4 góc ngoài của tứ giác lần lượt là : 180 - a ; 180 - b ; 180 - c ; 180 - d
Vậy 4 góc ngoài của tứ giác là : 180 - a + 180 - b + 180 - c + 180 - d
= ( 180 + 180 + 180 + 180 ) - ( a + b + c + d )
= 720o - 360o ( tổng 4 góc của tứ giác )
= 360o
Vậy tổng 4 góc ngoài của tứ giác là 360o
Tính tổng các góc ngoài của tứ giác (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) ?
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính các góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
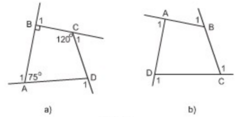
a) + Góc ngoài tại A là góc A1:
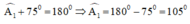
+ Góc ngoài tại B là góc B1:
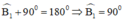
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
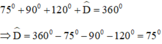
Lại có:
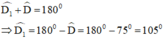
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
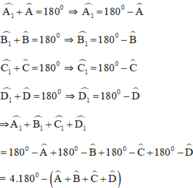
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
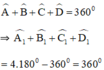
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.