Question

Cho tứ giác ABCD. Chứng minh rằng tổng hai góc ngoài tại các đỉnh A và C bằng tổng hai góc trong tại các đỉnh B và D.

Answer 1

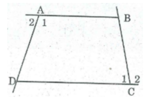
* Gọi ∠ A 1 ,  ∠ C 1 là góc trong của tứ giác tại đỉnh A và C,  ∠ A 2 ,  ∠ C 2 là góc ngoài tại đỉnh A và C.

Ta có:  ∠ A 1 +  ∠ A 2  = 180 0  (2 góc kề bù)

⇒  ∠ A 2 =  180 0  -  ∠ A 1

∠ C 1 +  ∠ C 2 =  180 0  (2 góc kề bù) ⇒  ∠ C 2 =  180 0  -  ∠ C 1

Suy ra:  ∠ A 2 +  ∠ C 2 =  180 0  -  ∠ A 1 + 180o -  ∠ C 1 =  360 0  – ( ∠ A 1  +  ∠ C 1 ) (1)

* Trong tứ giác ABCD ta có:

∠ A 1 +  ∠ B +  ∠ C 1  + ∠ D =  360 0  (tổng các góc của tứ giác)

⇒  ∠ B +  ∠ D =  360 0  - ( ∠ A 1  +  ∠ C 1 ) (2)

Từ (1) và (2) suy ra:  ∠ A 2 +  ∠ C 2  =  ∠ B +  ∠ D