Cho hai đường thẳng d1 2x - 3y +1 = 0 và d2 -4x + 6y -3 = 0
viết đường thẳng // với d1 và d2
Cho điểm A(1; 3) và hai đường thẳng d 1 : 2 x − 3 y + 4 = 0 , d 2 : 3 x + y = 0 . Số đường thẳng qua A và tạo với d 1 , d 2 các góc bằng nhau là
A.1
B.2
C.4
D.Vô số
ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.
(Bài này làm như thế nào vậy ạ???)
Cho hai đường thẳng (d2): 4x+3y-23=0 và (d1): y=1, biết đường thẳng d là đường phân giác góc tù tạo bởi hai đường thẳng d1 và d2. Phương trình đường thẳng d là?
A. 2x-y+9=0
B. -2x-y+9=0
C. 2x+y+9=0
D. 2x-y-9=0
Cho hai đường thẳng d1 : x+ y -1= 0 và d2 : x- 3y + 3= 0. Phương trình đường thẳng d đối xứng với d1 qua đường thẳng d2 là:
A.x-7y +1 =0
B.x+7y +1= 0
C. 7x+y+1= 0
D. 7x-y+1= 0
Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
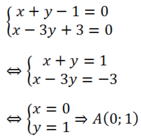
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
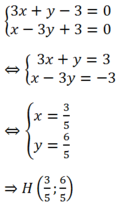
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
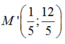
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương 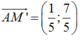
=> vectơ pháp tuyến 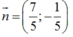
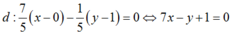
Cho hai đường thẳng d 1 : 6 x − 3 y + 4 = 0 , d 2 : 2 x − y + 3 = 0 . Bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là
A. 3 5
B. 3 5
C. 5 6
D. 5 3
ĐÁP ÁN C
Ta có: 6 2 = − 3 − 1 ≠ 4 3 nên d1 // d2.
Ta có: d 2 : 2 x − y + 3 = 0 ⇔ 6 x − 3 y + 9 = 0
Do d1 // d2. nên khoảng cách hai đường thẳng d1và d2 chính là đường kính của đường tròn.
Suy ra, bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là
R = 1 2 d d 1 , d 2 = 1 2 9 − 4 6 2 + − 3 2 = 5 6
trong mặt phẳng tọa độ Oxy,cho hai đường thẳng d1:2x-y+5=0,d2:3x+6y-1=0 và điểm P(-2,0).Gọi A là giao điểm của d1 và d2.Khi đó đường thẳng d đi qua P và cùng với d1,d2 tạo thành một tam giác cân đỉnh A có phương trình là?
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
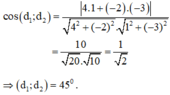
Cho hai đường thẳng: ax-3y=7 (d1) và 3x-6y=b+2(d2). Biết (d1) và (d2) trùng nhau. Tính a+b
Cho hai đường thẳng d1 : x+ 2y -1 = 0 và d2 : x- 3y +3 = 0. Phương trình đường thẳng d đối xứng với d1 qua là: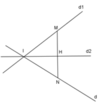
A. x -3y- 2= 0
B.x+ 3y+1= 0
C. 3x-y=1= 0
D. x-3y+ 3=0
Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
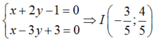
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
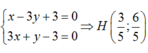
Phương trình đường thẳng
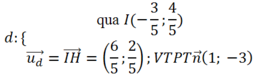
có dạng:
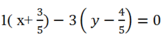
hay x-3y + 3= 0
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng d 1 : 2 x + 3 y + 1 = 0
và d 2 : x - y - 2 = 0 Có bao nhiêu phép tịnh tiến biến d 1 thành d 2
A.Vô số
B.4
C.1
D.0
Chọn D.
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2