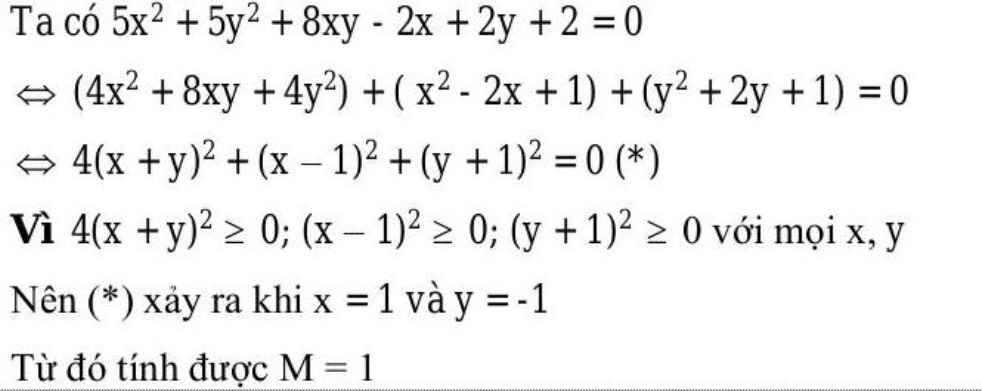Cho 2 số thực x và y thoả x+y=1 Tính giá trị biểu thức: A=x⁴-2x³-2x²y²-2y³+x²+y²+y⁴

Những câu hỏi liên quan
cho các số x,y thoả mãn đẳng thức 5x^2 + 5y^2 +8xy -2x +2y+2=0 tính giá trị các biểu thức M=(x+y)^2017 + (x-2)^2008 +(y+1)^2009
Ta có\(5x^2+5y^2+8xy-2x+2y+2=0\Leftrightarrow4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
<=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
mà \(\hept{\begin{cases}4\left(x+y\right)^2\ge0\\\left(y+1\right)^2\ge0\\\left(x-1\right)^2\ge0\end{cases}\Rightarrow}4\left(x+y\right)^2+\left(y+1\right)^2+\left(x-1\right)^2\ge0\)
dâu = xảy ra <=>\(\hept{\begin{cases}x=1\\y=1\end{cases}}\)
rồi bạn thay vào và tự tính M nhé !
^_^
Đúng 0
Bình luận (0)
cho các số thực dương X,y thỏa mãn x<y và\(3x^2\)+\(2y^2\)=5xy.Tính giá trị của biểu thức S=\(\dfrac{y+2x}{y-2x}\)
\(3x^2+2y^2=5xy\)
\(\Leftrightarrow3x^2+2y^2-5xy=0\)
\(\Leftrightarrow2\left(x^2-2xy+y^2\right)+x^2-xy=0\)
\(\Leftrightarrow2\left(x-y\right)^2+x\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[2\left(x-y\right)+x\right]=0\)
\(\Leftrightarrow\left(x-y\right)\left(3x-2y\right)=0\)
\(\Leftrightarrow3x-2y=0\Leftrightarrow x=\dfrac{2y}{3}\) Thay vào S
\(\Rightarrow S=\dfrac{y+\dfrac{4y}{3}}{y-\dfrac{4y}{3}}=-7\)
Đúng 0
Bình luận (0)
a,cho các số x,y,z khác 0 thoả mãn
\(x-2y+\frac{z}{y}=z-2x+\frac{y}{x}=x-2z-\frac{y}{z}\).Tính giá trị biểu thức A=\(\left(1+\frac{y}{x}\right)\times\left(1+\frac{y}{x}\right)=\left(1+\frac{x}{z}\right)+2020\)
b, tìm các số tự nhiên x,y thoả mãn xy+4x=35+5y
c, tìm các số tự nhiên x,y thoả mãn 2^/x/+y^2+y=2x+1
Bài 4:Cho các số x,y thoả mãn đẳng thức 5x2+5y2+8xy-2x+2y+2=0
Tính giá trị của biểu thức:M=(x+y)2019 + (x-2)2020 + (y+1)2021
cho các số x,y thoả mãn đẳng thức 5x2+5y2+8xy-2x+2y+2=0
Tính giá trị của biểu thức M=(x+y)2015+(x-2)2016+(y+1)2017
Mọi người giúp nhóc em với ạ![]()
\(5x2+5y2+8xy-2x+2y+2=0\)
(=) \((4x^2 + 8xy + 4y^2) + (x^2 - 2x +1) + (y^2 + 2y +1) = 0 \)
(=) \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
Ta có \(\begin{cases} 4(x+y)^2 ≥ 0 \\ (x-1)^2 ≥ 0 \\ (y+1)^2 ≥ 0 \end{cases} \)
=> \(4(x+y)^2 + (x-1)^2 + (y+1)^2 ≥ 0 \)
Vậy để \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
(=) \(\begin{cases} 4(x+y)^2 = 0 \\ (x-1)^2 = 0 \\ (y+1)^2 = 0 \end{cases} \)
(=) \(\begin{cases} x = -y \\ x = 1 \\ y = -1 \end{cases} \)
(=) \(\begin{cases} x = 1 \\ y = -1 \end{cases} \)
Vậy \(M=(x+y)^{2015}+(x-2)^{2016}+(y+1)^{2017} M=(1-1)^{2015} + (1-2)^{2016} + (-1+1)^{2017} M=0^{2015} + (-1)^{2016} +0^{2017} M= 1 \)Vậy M = 1
Đúng 0
Bình luận (0)
Cho các số x,y là các số thực thoả mãn: \(\frac{x-y}{x^2+xy}\)+ \(\frac{x+y}{x^2-xy}\)=\(\frac{3x-y}{x^2-y^2}\)
Tính giá trị biểu thức Q= \(\frac{x^3+3y^3}{x^2y+y^2x}\)
a, cho x, y là 2 số thoả mãn (2x - y + 7)^{2022} + |x - 1|^{2023} ≤ 0. Tính giá trị của biểu thức: P x^{2023} + (y - 10)^{2023}b, Tìm số tự nhiên x, y biết 25 - y^2 8(x 2023)^2 c, Tìm giá trị nhỏ nhất của biểu thức: P (|x - 3| + 2)^2 + |y + 3| + 2019d, Tìm cặp số nguyên x, y biết: (2 - x)(x + 1) |y + 1|
Đọc tiếp
a, cho x, y là 2 số thoả mãn (2x - y + 7)\(^{2022}\) + |x - 1|\(^{2023}\) ≤ 0. Tính giá trị của biểu thức: P = x\(^{2023}\) + (y - 10)\(^{2023}\)
b, Tìm số tự nhiên x, y biết 25 - y\(^2\) = 8(x = 2023)\(^2\)
c, Tìm giá trị nhỏ nhất của biểu thức: P = (|x - 3| + 2)\(^2\) + |y + 3| + 2019
d, Tìm cặp số nguyên x, y biết: (2 - x)(x + 1) = |y + 1|
a: \(\left(2x-y+7\right)^{2022}>=0\forall x,y\)
\(\left|x-1\right|^{2023}>=0\forall x\)
=>\(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}>=0\forall x,y\)
mà \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}< =0\forall x,y\)
nên \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}=0\)
=>\(\left\{{}\begin{matrix}2x-y+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x+7=9\end{matrix}\right.\)
\(P=x^{2023}+\left(y-10\right)^{2023}\)
\(=1^{2023}+\left(9-10\right)^{2023}\)
=1-1
=0
c: \(\left|x-3\right|>=0\forall x\)
=>\(\left|x-3\right|+2>=2\forall x\)
=>\(\left(\left|x-3\right|+2\right)^2>=4\forall x\)
mà \(\left|y+3\right|>=0\forall y\)
nên \(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|>=4\forall x,y\)
=>\(P=\left(\left|x-3\right|+2\right)^2+\left|y-3\right|+2019>=4+2019=2023\forall x,y\)
Dấu '=' xảy ra khi x-3=0 và y-3=0
=>x=3 và y=3
Đúng 0
Bình luận (0)
CHO 2 SỐ THỰC X;Y THỎA MÃN X^2 +Y^2 =1.GIÁ TRỊ BIỂU THỨC A=X^4+2X^2Y^2+X^2+Y^4+Y^2 LÀ:
1) Cho a+b=-20 và x-y=-6
Tính giá trị bt A=ax-by+bx-ay
2) Đơn giản biểu thức A=-2(x+3)+|-2x|+|3x|+7x
3) Tìm các số nguyên x,y thoả mãn: x(y+2)+2y(x+3)=-7