Tìm các giá trị nguyên của x để biểu thức nhận giá trị nguyên 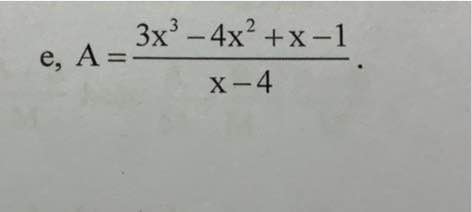

Những câu hỏi liên quan
Cho biểu thức
M=căn x +1/2
A)Tìm các giá trị nguyên của x để M nhận giá trị nguyên
B)Tìm giá trị lớn nhất của biểu thức M
c)Tìm các giá trị nguyên của x để A nhận giá trị nguyên
a) Tìm các giá trị nguyên của x để biểu thức Mdfrac{8x+1}{4x-1}nhận giá trị nguyênb) Tìm giá trị nguyên của biến x để biểu thức Adfrac{5}{4-x}có giá trị lớn nhấtc) Tìm giá trị nguyên của biến x để biểu thức Bdfrac{8-x}{x-3}có giá trị nhỏ nhất(Hơi khó mọi người giúp mình với ạ)
Đọc tiếp
a) Tìm các giá trị nguyên của \(x\) để biểu thức M=\(\dfrac{8x+1}{4x-1}\)nhận giá trị nguyên
b) Tìm giá trị nguyên của biến \(x\) để biểu thức \(A=\dfrac{5}{4-x}\)có giá trị lớn nhất
c) Tìm giá trị nguyên của biến \(x\) để biểu thức \(B=\dfrac{8-x}{x-3}\)có giá trị nhỏ nhất
(Hơi khó mọi người giúp mình với ạ)
a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow11⋮4x-5\)
Vì \(x\in Z\) nên \(4x-5\in Z\)
\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)
Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).
b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)
Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)
4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)
Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất
\(\Rightarrow4-x=1\Rightarrow x=3\)
\(\Rightarrow A=\dfrac{5}{4-3}=5\)
Vậy MaxA = 5 tại x = 3
c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).
Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)
Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất
\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất
Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\)
x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)
Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất
\(\Rightarrow x-3=-1\Rightarrow x=2\)
\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)
Vậy MaxB = -6 tại x = 2.
Đúng 1
Bình luận (1)
a) Để M nhận giá trị nguyên thì \(8x+1⋮4x-1\)
\(\Leftrightarrow8x-2+3⋮4x-1\)
mà \(8x-2⋮4x-1\)
nên \(3⋮4x-1\)
\(\Leftrightarrow4x-1\inƯ\left(3\right)\)
\(\Leftrightarrow4x-1\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow4x\in\left\{2;0;4;-2\right\}\)
\(\Leftrightarrow x\in\left\{\dfrac{1}{2};0;1;-\dfrac{1}{2}\right\}\)
mà x là số nguyên
nên \(x\in\left\{0;1\right\}\)
Vậy: \(x\in\left\{0;1\right\}\)
Đúng 0
Bình luận (0)
Tìm các giá trị nguyên của x để biểu thức nhận giá trị nguyên 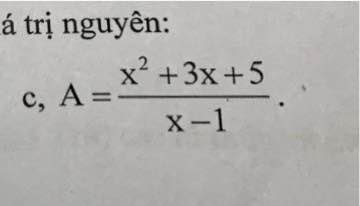
Để A nguyên thì \(x^2-x+4x-4+9⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(x\in\left\{2;0;4;-2;10;-8\right\}\)
Đúng 1
Bình luận (0)
Tìm các giá trị nguyên của x để biểu thức nhận giá trị nguyên 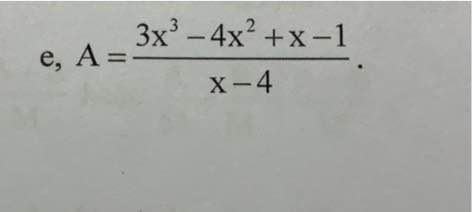
\(A=\dfrac{3x^3-4x^2+x-1}{x-4}=\dfrac{3x^2\left(x-4\right)+8x\left(x-4\right)+33\left(x-4\right)+131}{x-4}=\dfrac{\left(x-4\right)\left(3x^2+8x+33\right)+131}{x-4}=3x^2+8x+33+\dfrac{131}{x-4}\in Z\)
\(\Rightarrow\left(x-4\right)\inƯ\left(131\right)=\left\{-131;-1;1;131\right\}\)
\(\Rightarrow x\in\left\{-127;3;5;135\right\}\)
Đúng 1
Bình luận (0)
Tìm các giá trị nguyên của x để biểu thức nhận giá trị nguyên 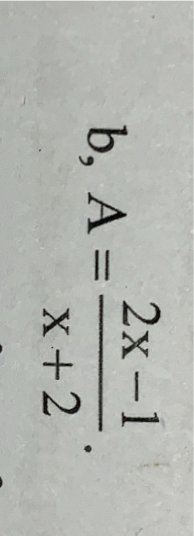
\(A=\dfrac{2x-1}{x+2}\)
\(\Rightarrow A=\dfrac{2x+4-5}{x+2}\)
\(\Rightarrow A=\dfrac{2\left(x+2\right)-5}{x+2}\)
\(\Rightarrow A=\dfrac{2\left(x+2\right)}{x+2}-\dfrac{5}{x+2}\)
\(\Rightarrow A=2-\dfrac{5}{x+2}\)
\( Để.A\in Z.mà.2\in Z\Rightarrow\dfrac{5}{x+2}\in Z\Rightarrow5⋮\left(x+2\right)\Rightarrow x+2\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Ta có bảng:
| x+2 | -1 | -5 | 1 | 5 |
| x | -3 | -7 | -1 | 3 |
Vậy \(x\in\left\{-3;-7;-1;3\right\}\)
Đúng 2
Bình luận (2)
tìm các giá trị nguyên của x để biểu thức B=1-2x/x+3 nhận giá trị nguyên
1 - 2x = -(2x - 1)
= -(2x + 6 - 7)
= -(2x + 6) + 7
= -2(x + 3) + 7
Để B nguyên thì (1 - 2x) ⋮ (x + 3)
⇒ 7 ⋮ (x + 3)
⇒ x + 3 ∈ Ư(7) = {-7; -1; 1; 7}
⇒ x ∈ {-10; -4; -2; 4}
Đúng 1
Bình luận (1)
Cho biểu thức A= \(\dfrac{x-3}{2x+3}\) . Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
Lời giải:
Để $A$ nguyên thì \(x-3\vdots 2x+3\)
\(\Leftrightarrow 2(x-3)\vdots 2x+3\)
\(\Leftrightarrow 2x-6\vdots 2x+3\Leftrightarrow 2x+3-9\vdots 2x+3\)
\(\Leftrightarrow 9\vdots 2x+3\Rightarrow 2x+3\in\left\{\pm 1;\pm 3;\pm 9\right\}\)
\(\Rightarrow x\in \left\{-2; -1; 0; -3; -6; 3\right\}\)
Đúng 0
Bình luận (0)
Cho biểu thức A=x^2+3/x-2
a)Tìm điều kiện của x để giá trị của biểu thức A không xác định được
b)với nhứng giá trị nào của x thì biểu thức a nhận giá trị là số âm
c) Tìm tất cả các số nguyên x để biểu thức A nhận giá trị nguyên
Tìm các giá trị nguyên x để biểu thức A= 3x+1/x+2 nhận giá trị nguyên
`A=[3x+1]/[x+2]=[3x+6-5]/[x+2]=3-5/[x+2]`
Để `A` nhận giá trị nguyên thì `3-5/[x+2] in ZZ`
`=>x+2 in Ư_5`
Mà `Ư_5 ={+-1;+-5}`
`@x+2=1=>x=-1`
`@x+2=-1=>x=-3`
`@x+2=5=>x=3`
`@x+2=-5=>x=-7`
Đúng 4
Bình luận (1)




















