Chứng minh:
AMI = NMK
. Từ đó suy ra ba điểm I, M, K thẳng hàng

Những câu hỏi liên quan
Cho ∆ABC, gọi M là trung điểm cạnh BC. Trên tia AM lấy điểm N sao cho
AM = MN.
a) Chứng minh: ∆AMC = ∆NMB
b) Chứng minh: AB // CN.
Trên cạnh AC lấy điểm I và trên cạnh BN lấy điểm K sao cho AI = NK. Chứng minh:
AMI
= NMK
. Từ đó suy ra ba điểm I, M, K thẳng hàng
Cho tam giác ABC cân tại A. Gọi M,N lần lượt là trung điểm AB và AC: BN cắt CN tại G. Trên tia đối của tia NB lấy điểm K sao cho NK=NG. a) Chứng minh tam giác ANG = tamgiac CNK. Từ đó suy ra AG//CK.
b Trên tia đối của tia CB lấy điểm E sao cho CE =CB ; Em cắt AC tại I, chứng minh A,K, E thẳng hàng. Từ đó suy ra I là trọng tam tam ABE
Giúp mình câu b với mọi người. Thanks
Cho ∆ABC vuông tại A có số đo góc B bằng 53°.
A) tính số đo góc C
B)trên cạnh BC, lấy điểm D sao cho BD =BA. Tia phân giác của góc B cắt AC tại điểm E. Chứng minh ∆BEA =∆ BED. Từ đó suy ra ED vuông góc với BC.
C) trên tia BA lấy điểm M sao cho BM = BC . chứng minh ∆BEM=∆BEC.
D) chứng minh MD vuông góc với BC Từ đó suy ra M,E,D thẳng hàng
Xin lỗi mọi người nhìn hơi rối tí nhưng mà giải giúp em với ạ
Cho ∆ABC có hai đường trung tuyến BD và CE. Gọi M là điểm đối xứng với B qua D; N là điểm đối xứng với C qua E.
a) Chứng minh: ABCM là hình bình hành. Từ đó suy ra: AM = BC .
b) Chứng minh: AN // BC . Từ đó suy ra: A, M, N thẳng hàng và M đối xứng với N qua A.
c) Gọi G là trọng tâm tam giác ABC. P đối xứng với G qua D ; Q đối xứng với G qua E. Chứng minh rằng: BCPQ là hình bình hành.
a: Xét tứ giác ABCM có
D là trung điểm của đường chéo AC
D là trung điểm của đường chéo MB
Do đó: ABCM là hình bình hành
Suy ra: AM=BC và AM//BC
b: Xét tứ giác ACBN có
E là trung điểm của đường chéo AB
E là trung điểm của đường chéo NC
Do đó: ACBN là hình bình hành
Suy ra: AN//BC và AN=BC
Ta có: AN//BC
AM//BC
mà AN và AM có điểm chung là A
nên N,A,M thẳng hàng
mà NA=AM(=BC)
nên M đối xứng với N qua A
Đúng 1
Bình luận (0)
Cho tam giác ABC có AC=2AB. Trên cạnh AC lấy điểm M sao cho AM=AB. Tia phân giác cúa góc BAC cắt BM tại I
a) Chứng minh: Tam giác ABI=tam giác AMI. Từ đó suy ra AI vuông góc với BM
b) Trên tia đối của tia BA lấy điểm D sao cho B là trung điểm của AD. Chứng minh DC song song với BM
c) Kéo dài AI cắt cạnh BC tại K và cắt CD tại E. Chứng minh: D,K,M thẳng hàng
Giúp mình câu b và c với ạ
b) Vì AC=2AB
AB=BD
=>AC=AD
Xét tam giác ACE và tam giác ADE có:
AC=AD ( chứng minh trên )
^CAE=^EAD ( tính chất phân giác )
AE chung
=> tam giác ACE = tam giác ADE ( c.g.c )
=> ^CEA=^AED ( 2 góc tương ứng )
Mà ^CEA kề bù ^AED
=> ^CEA=^AED=90°
=> AE vuông góc CD
AI và AE là 2 tia trùng nhau
=> AI vuông góc CD
Vì AI vuông góc BM
Mà AI vuông góc CD
<=> BM // CD
Chúc bạn học tốt!
Vì mình không tìm được cách gõ góc nên kí hiệu ^ là góc nhé! Mong bạn thông cảm
Bài 1:Cho tam giác ABC vuông tại A có góc B bằng 60 độ . Vẽ AH vuônggóc với BC tại H. Trên cạnh AC lấy điểm D sao cho AD AH. Gọi I là trung điểmcủa cạnh HD.a) Chứng minh: Tam giác AHI tam giácADI. Từ đó suy ra AI vuông góc HDb) Tia AI cắt cạnh HC tại điểm K. Chứng minh tam giác AHK tam giác ADK từ đó suyra AB // KD.c) Trên tia đối của tia HA lấy điểm E sao cho HE AH. Chứng minh HB HK và ba điểm D, K, E thẳng hàng.Mn giúp vs ạ
Đọc tiếp
Bài 1:Cho tam giác ABC vuông tại A có góc B bằng 60 độ . Vẽ AH vuông
góc với BC tại H. Trên cạnh AC lấy điểm D sao cho AD = AH. Gọi I là trung điểm
của cạnh HD.
a) Chứng minh: Tam giác AHI= tam giácADI. Từ đó suy ra AI vuông góc HD
b) Tia AI cắt cạnh HC tại điểm K. Chứng minh tam giác AHK= tam giác ADK từ đó suy
ra AB // KD.
c) Trên tia đối của tia HA lấy điểm E sao cho HE = AH. Chứng minh HB =
HK và ba điểm D, K, E thẳng hàng.
Mn giúp vs ạ
Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC. Chứng minh rằng các đường thẳng IK và ED song song với mặt phẳng (AFC). Từ đó suy ra ba vecto
A
F
→
,
I
K
→
,
E
D
→
đồng phẳng.
Đọc tiếp
Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC. Chứng minh rằng các đường thẳng IK và ED song song với mặt phẳng (AFC). Từ đó suy ra ba vecto A F → , I K → , E D → đồng phẳng.
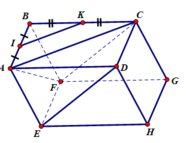
I và K lần lượt là trung điểm của các cạnh AB và BC ⇒ IK là đường trung bình của ∆ABC nên IK // AC ⊂ (AFC) ⇒ IK // (AFC)
hình hộp ABCD.EFGH nên các mặt của hình hộp là hình bình hành.
Suy ra: EF// CD(cùng // GH) và EF = CD ( cùng = GH)
EFCD là hình bình hành
⇒ ED // CF
Nên ED // (AFC)
⇒ ba vecto A F → , I K → , E D → đồng phẳng (vì giá của chúng song song với một mặt phẳng)
Đúng 0
Bình luận (0)
Bài 3 Cho tam giác ABC có AB AC. M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD MA.a. Chứng minh tam giác AMB tam giác DMC từ đó suy ra AB //CD.b. Từ A kẻ AH vuông góc BC tại H. Gọi N là trung điểm của AC. Từ N kẻ đường thẳng song song với BC cắt AB tại E. Chứng minh rằng EN vuông góc AH.c. Trên tia đối của tia NE lấy K sao cho NK NE. Chứng minh ba điểm D, C, K thẳng hàng.
Đọc tiếp
Bài 3 Cho tam giác ABC có AB < AC. M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Chứng minh tam giác AMB = tam giác DMC từ đó suy ra AB //CD.
b. Từ A kẻ AH vuông góc BC tại H. Gọi N là trung điểm của AC. Từ N kẻ đường thẳng song song với BC cắt AB tại E. Chứng minh rằng EN vuông góc AH.
c. Trên tia đối của tia NE lấy K sao cho NK = NE. Chứng minh ba điểm D, C, K thẳng hàng.
Cho tam giác ABC vuông tại A, trên tia đối của tia AB lấy điểm D sao cho AB ADa) Biết; AC 8cm, BC 10cm. Tính AB, BD. So sánh các góc của tam giác ABCb) Chứng minh: Tam giác ABC tam giác ADC, từ đó suy ra tam giác BCD cânc) Gọi N là trung điểm của BC, đường thẳng qua B song song với CD cắt DN tại K. Chứng minh; DN NK. Từ đó suy ra 2.DN DC + DBd) Đường thẳng qua A song sowng với BC cắt CD tại M, gọi G là giao điểm của AC và DN, Chứng minh: ba điểm B, G, M thẳng hàng.Mình cần lời giải chi ti...
Đọc tiếp
Cho tam giác ABC vuông tại A, trên tia đối của tia AB lấy điểm D sao cho AB = AD
a) Biết; AC = 8cm, BC = 10cm. Tính AB, BD. So sánh các góc của tam giác ABC
b) Chứng minh: Tam giác ABC = tam giác ADC, từ đó suy ra tam giác BCD cân
c) Gọi N là trung điểm của BC, đường thẳng qua B song song với CD cắt DN tại K. Chứng minh; DN = NK. Từ đó suy ra 2.DN < DC + DB
d) Đường thẳng qua A song sowng với BC cắt CD tại M, gọi G là giao điểm của AC và DN, Chứng minh: ba điểm B, G, M thẳng hàng.
Mình cần lời giải chi tiết các bạn giúp mình nhé














