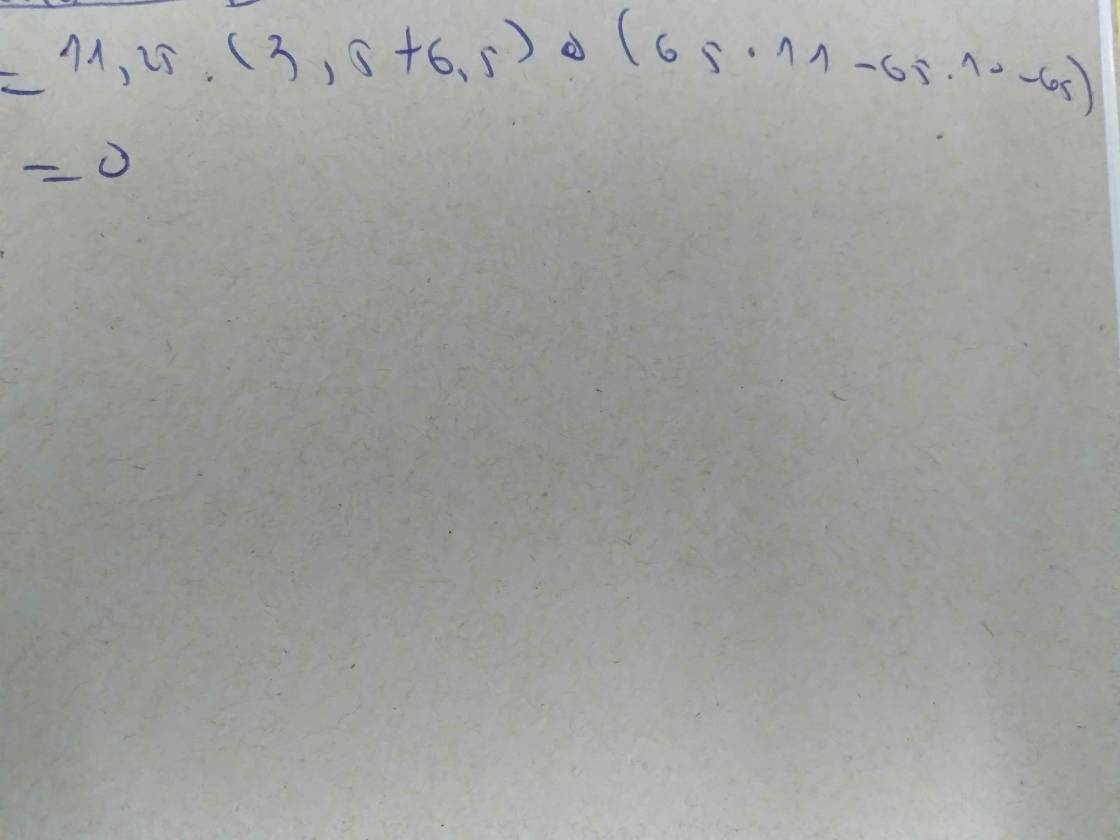8,3755

8,3755

C

C

C

\(\left(3,5\times11,25+11,25\times6,5\right)\times\left(65\times11-65:0,1:65\right)\\ =\left[11,25\times\left(3,5+6,5\right)\right]\times\left(65\times11-10\right)\\ =\left[11,25\times10\right]\times\left[715-10\right]\\ =112,5\times705\\ =79312,5\)

35 x 34 + 35 x 65 + 65 x 75 + 65 x 45

= ( 35 x 34 + 35 x 65 ) + ( 65 x 75 + 65 x 45 )

= 35 x ( 34 + 65 ) + 65 x ( 75 + 45 )

= 35 x 99 + 65 x 120

= 3465 + 7800

= 11265

\(35.34+35.65+65.75+65.45\)

=\(35.\left(34+65\right)+65.\left(75+45\right)\)

= 35. 99 +65.120

=3465 + 7800

= 11265

\(\dfrac{x+1}{65}+\dfrac{x+3}{63}\) = \(\dfrac{x+5}{61}\) + \(\dfrac{x+7}{59}\)

<=> \(\dfrac{x+1}{65}+1+\dfrac{x+3}{63}+1\) = \(\dfrac{x+5}{61}\) + 1 + \(\dfrac{x+7}{59}\) + 1

<=> \(\dfrac{x+66}{65}+\dfrac{x+66}{63}\) = \(\dfrac{x+66}{61}\) + \(\dfrac{x+66}{59}\)

<=> \(\dfrac{x+66}{65}+\dfrac{x+66}{63}\) - \(\dfrac{x+66}{61}\) - \(\dfrac{x+66}{59}\) = 0

<=> (x + 66) . (\(\dfrac{1}{65}+\dfrac{1}{63}+\dfrac{1}{61}+\dfrac{1}{59}\)) = 0

<=> x + 66 = 0

<=> x = -66

hình như bn sai đề đúng ko

3,527 + 65 x 73 + 65 x 27 + 3,573

= 3,527 + 65 x ( 73 + 27 ) + 3,573

= 3,527 + 65 x 100 + 3,573

= 3,527 + 6500 + 3,573

= 6507,1

\(3,527+65\times73+65\times27+3,573\\ =\left(3,527+3,573\right)+65\times\left(73+27\right)\\ =7,1+65\times100\\ =7,1+6500\\ =6507,1\)

A =3,527 + 65 \(\times\) 73 + 65 \(\times\) 27 + 3,573

A = (3,527 + 3,573) + (65 \(\times\) 73 + 65 \(\times\) 27)

A = 7,1 + 65 \(\times\) ( 73 + 27)

A = 7,1 + 65 \(\times\) 100

A = 7,1 + 6500

A = 6507,1

20,10x35-19,45x65+20,10x65-19,45x35

=(35+65)x20,10+(35+65)x19,45

=100x20,10-100x19,45

=100x(20,10-19,45)

=100x0,65=65

Đặt \(\hept{\begin{cases}\sqrt[3]{65+x}=a\\\sqrt[3]{65-x}=b\end{cases}}\)

\(\Rightarrow a^2+4b^2=5ab\)

\(\Leftrightarrow\left(b-a\right)\left(4b-a\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}a=b\\a=4b\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}\sqrt[3]{65+x}=\sqrt[3]{65-x}\\\sqrt[3]{65+x}=4\sqrt[3]{65-x}\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}65+x=65-x\\65+x=4\left(65-x\right)\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=39\end{cases}}\)

Đặt \(a=\sqrt[3]{\left(65-x\right)};b=\sqrt[3]{65+x}\)

pt<=> \(a^2+b^2=ab\Leftrightarrow\begin{cases}a=0\\b=0\end{cases}\)

nên vô lí 

PT vô nghiệm