cho đường tròn (O) có đường kính AB vuông dây cung tại E
chứng minh : CD2 = 4AE - BE
Những câu hỏi liên quan
Bài 4: Cho đường tròn tâm O đường kính AC. Trên đoạn thẳng OC lấy điểm B và vẽ đường tròn O’ có đường kính BC. Gọi M là trung điểm của AB, qua M kẻ dây cung vuông góc với AB cắt đường tròn O tại D và E. Nối CD cắt đường tròn O’ tại Ia/ Chứng minh DAEB là hình gì?b/ Chứng minh MI MD và MI là tiếp tuyến của đường tròn O’c/ Gọi H là hình chiếu của I trên BC. Chứng minh CH.MB BH.MCMn giúp em với ạ, cảm ơn mn nhìu :
Đọc tiếp
Bài 4: Cho đường tròn tâm O đường kính AC. Trên đoạn thẳng OC lấy điểm B và vẽ đường tròn O’ có đường kính BC. Gọi M là trung điểm của AB, qua M kẻ dây cung vuông góc với AB cắt đường tròn O tại D và E. Nối CD cắt đường tròn O’ tại I
a/ Chứng minh DAEB là hình gì?
b/ Chứng minh MI = MD và MI là tiếp tuyến của đường tròn O’
c/ Gọi H là hình chiếu của I trên BC. Chứng minh CH.MB= BH.MC
Mn giúp em với ạ, cảm ơn mn nhìu :>
Chon đường tròn O ,đường kính ab=2r .C là điểm bất kì trên đường tròn cắt đường thẳng BC tại I.Chứng minh tứ giác AOMI nội tiếp.Vẽ dây cung Ak vuông góc OI tại E .Chứng minh I k là tiếp tuyến của đường tròn o .Vẽ dây cung AD song song BC .Chứng minh ba điểm D,M,K thẳng hàng
Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K. 1.Chứng minh tứ giác BMFE nội tiếp. 2.Chứng minh BF vuông góc với AK và EK.EF = EA.EB 3.Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Xét (O) có
\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AEB}=90^0\)
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{FIB}=180^0\)
nên BEFI là tứ giác nội tiếp
hay B,E,F,I cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có ABAC, đường ca AH. Vẽ tròn đường kính BH cắt AB tại E, đường tròn đường kính HC cắt AC tại F.a) Chứng minh tứ giác AEHF nội tiếp đường tròn ? Tìm tâm và đường kính của đường tròn ngoại tiếp tứ giác AEHFb) Cứng minh AE.AB AF.ACc) Chứng minh bốn điểm B, E, F, C cùng nằm trên một đường trònd) Biết góc ABC bằng 30o, BH 4cm. tính tổng diện tích hình viên phân giới hạn bởi dây BE; dây HE và cung HE
Đọc tiếp
Cho tam giác ABC vuông tại A có AB>AC, đường ca AH. Vẽ tròn đường kính BH cắt AB tại E, đường tròn đường kính HC cắt AC tại F.
a) Chứng minh tứ giác AEHF nội tiếp đường tròn ? Tìm tâm và đường kính của đường tròn ngoại tiếp tứ giác AEHF
b) Cứng minh AE.AB = AF.AC
c) Chứng minh bốn điểm B, E, F, C cùng nằm trên một đường tròn
d) Biết góc ABC bằng 30o, BH =4cm. tính tổng diện tích hình viên phân giới hạn bởi dây BE; dây HE và cung HE
cho đường tròn (O) có đường kính BC =10cm , lấy điểm A trên đường tròn (O) sao cho AB = 6cm , kẻ tiếp tuyến của đường tròn (O) tại B cắt AC kéo dài tại D . a) Tính độ dài đoạn thẳng DC .b) vẽ dây cung BE vuông góc với OD tại H , chứng minh ^DOA=^DCH
Xem chi tiết
Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
c) Chứng minh H A 2 + H B 2 + C D 2 / 2 = 4 R 2
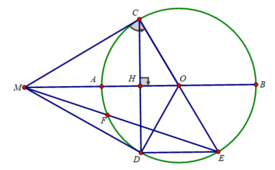
c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác
⇒ CH = HD = CD/2 ⇒ C H 2 = D H 2 = C D 2 / 4
Tam giác ACH vuông tại H có:
A H 2 + C H 2 = C A 2 ⇒ A H 2 + C D 2 / 4 = C A 2 (1)
Tam giác CHB vuông tại H có:
B H 2 + C H 2 = C B 2 ⇒ B H 2 + C D 2 / 4 = C B 2 (2)
Từ (1) và (2) ta có:
Đúng 0
Bình luận (0)
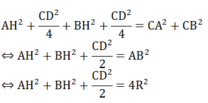
Cho đường tròn (O) đường kính AB, dây CD vuông góc với AB tại E (E nằm giữa A và O,E khác A và O). Lấy điểm M thuộc cung nhỏ BC sao cho cun MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.
a, Chứng minh tứ giác BMFE nội tiếp
b, Chứng minh BF vuông góc với AK và EK.EF=EA.EB
c, Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK=IF
a: góc AMB=1/2*sđ cung AB=90 độ
góc FEB+góc FMB=180 độ
=>FMBE nội tiếp
b: Xét ΔKAB có
AM,KE là đường cao
KE cắt AM tại F
=>F là trực tâm
=>BF vuông góc AK
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
a) \(\Delta ABE\)nội tiếp đường tròn đường kính \(AB\)
\(\Rightarrow\)\(\Delta ABE\perp E\)
\(\Rightarrow\)\(AEB\lambda=90\)độ
Tứ giác\(BEFI\)nội tiếp đường tròn đường kính \(FB\)