CHO ĐIỂM M NẰM TRONG TAM GIÁC ABC.CHỨNG MINH RẰNG:MA+MB+MC<AB+AC+BC

Những câu hỏi liên quan
Cho tam giác ABC,gọi M là một điểm nằm trong tam giác.Chứng minh rằng:MA+MB+MC<AB+AC+BC
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.a) So sánh MB + MC với BCb) Chứng minh
M
A
+
M
B
+
M
C
A
B
+
B
C
+
C
A
2
Đọc tiếp
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh M A + M B + M C > A B + B C + C A 2
Cho tam giác ABC, điểm M nằm trong tam giác. Chứng minh: MB+MC < AB+AC
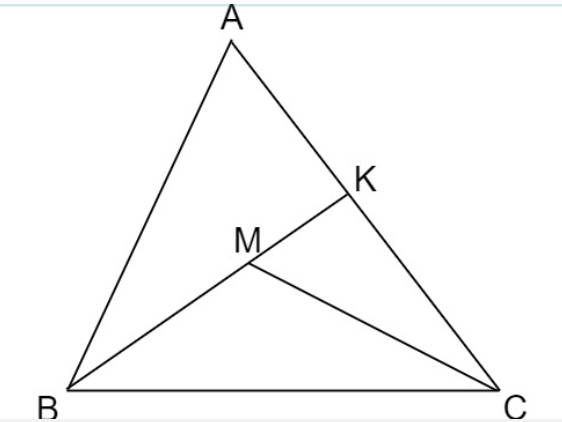
Kéo dài \(BM\) cắt \(AC\) tại \(K\)
Ta có: \(BK< AB+AK\) (bất đẳng thức t/g)
hay \(BM+MK< AB+AK\) \(\left(1\right)\)
Ta lại có: \(MC< MK+KC\) \(\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow BM+MK+MC< AB+AK+MK+KC\)
Hay \(BM+MC< AB+AK+KC\)
Hay \(BM+MC< AB+AC\)
Đúng 3
Bình luận (1)
Cho điểm M nằm trong tam giác ABC. 1) So sánh AB với MA + MB . 2) CMR: AB + AC + BC < 2(MA + MB + MC) . 3) Chứng minh rằng MA + MB +MC lớn hơn nửa chu vi tam giác ABC.
Cho điểm M nằm trong tam giác ABC. Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi tam giác ABC.
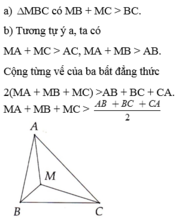
Trong ΔAMB, ta có:
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ΔAMC, ta có:
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ΔBMC, ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế (1), (2) và (3), ta có:
MA + MB + MA + MC + MB + MC > AB + AC + BC
⇔ 2(MA + MB + MC) > AB + AC + BC
Vậy MA + MB + MC > (AB + AC + BC) / 2
Đúng 1
Bình luận (0)
Cho tam giác đều ABC.Trong tam giác đều ABC lấy điểm M sao cho MB = MC và góc BMC =90 độ.
a)Chứng minh tam giác ABM = tam giác AMC
b)Trong tam giác BMC lấy điểm E sao cho góc EBC =góc ECM = 30 độ. Chứng minh tam giác MEC cân
c)Giả sử điểm M nằm trong tam giác ABC sao cho MA :MB :MC =3 :4 :5 . Tính góc AMB
mk ko bt lm câu b nha ~ xl
c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)
=> DM = AD = AM
Sau đó bạn chứng minh tam giác ADB = tam giác AMC (c.g.c) (cũng dễ thôi)
=> BD = MC (cặp cạnh tương ứng)
Ta có: DM = AM, BD = MC
=> DM : BM : BD = 3:4:5
=> tam giác BDM vuông tại M
=> góc AMB = 90o + 60o = 150o
a, Xét tam giác ABM và AMC có
BC=BA ( tam giác đều )
BMC=BMA=90độ
Góc C=A
=> ABM=AMC
Xem thêm câu trả lời
cho m là điểm nằm trong tam giác abc .
chứng minh: ma+mb+mc>ab+AC+BC
__________
2
$M$ là điểm nằm trong $ΔABC$
nên ta có các tam giác $ΔMAB;MAC;MBC$
Xét $ΔMAB$ có: $MA+MB>AB$ (quan hệ giữa 3 cạnh trong 1 tam giác;bất đẳng thức tam giác)
tương tự $ΔMAC$ có: $MA+MC>AC$
$ΔMBC$ có: $MB+MC>BC$
nên $MA+MB+MA+MC+MB+MC>AB+BC+CA$
suy ra $2.(MA+MB+MC)>AB+BC+CA$
hay $MA+MB+MC>\dfrac{AB+BC+CA}{2}$
Đúng 2
Bình luận (0)
Cho tam giác ABC và một điểm M nằm trong tam giác đó. Chứng Minh Rằng: MA+MB+MC > nửa chu vi tam giác ABC
Cho điểm M nằm trong tam giác ABC. Chứng minh rằng tổng MA + MB +MC lớn hơn nửa chu vi tam giác ABC ?
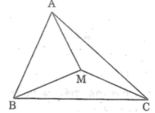
(h.45) Xét \(\Delta ABM:\)MA+MB>AB (1)
Xét \(\Delta AMC:\) MA+MC>AC (2)
Xét \(\Delta BMC:\) MB+MC>BC (3)
Cộng từng vế (1), (2), (3):
2(MA+MB+MC)>\(\text{AB+AC+BC}\)
Suy ra :
MA+MB+MC>\(\dfrac{\text{AB+AC+BC}}{2}\)
Đúng 1
Bình luận (0)