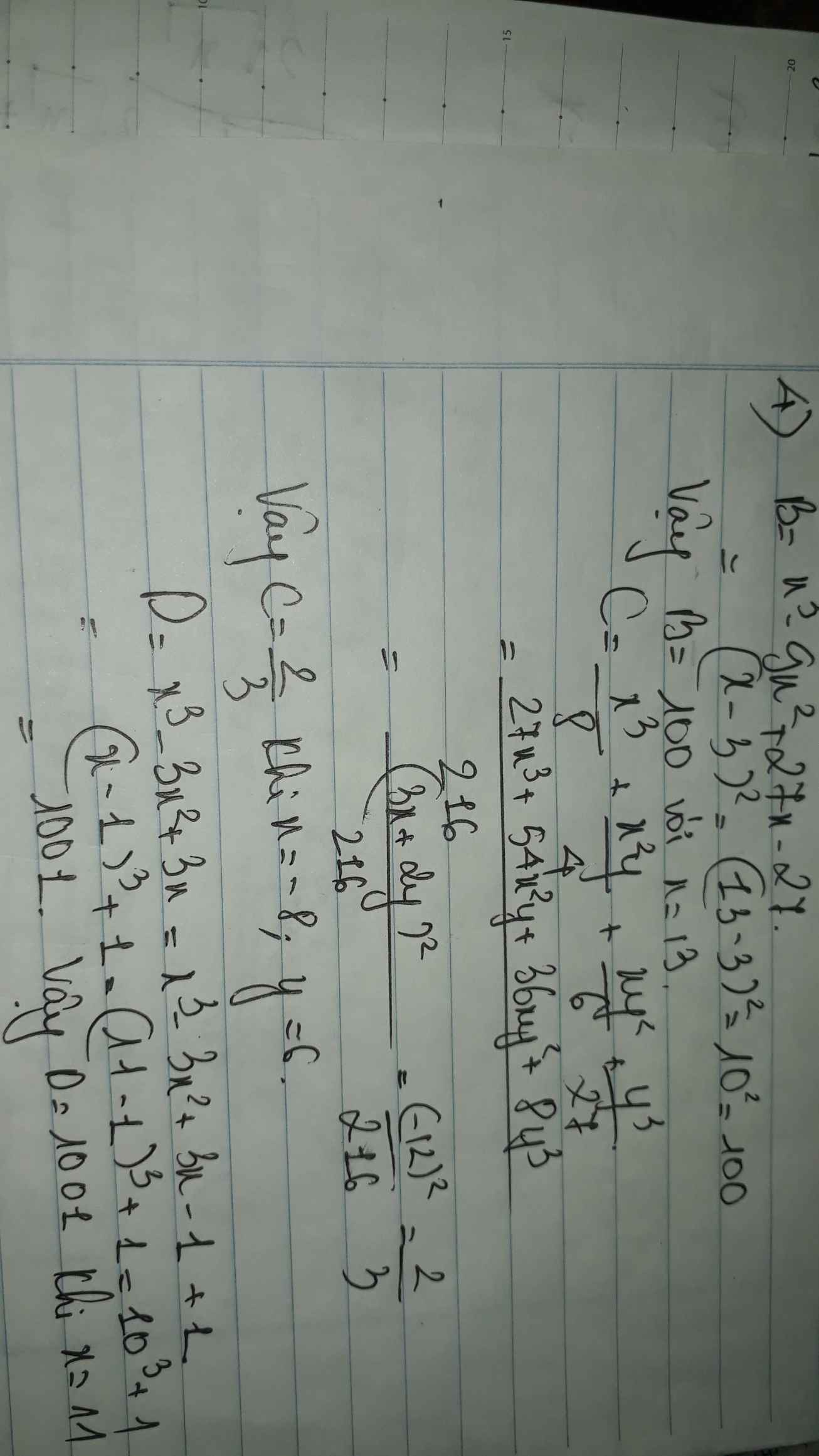\(\dfrac{1}{x-3}=\dfrac{2}{x+1}\Leftrightarrow x+1=\left(x-3\right)2\Leftrightarrow x+1-2x+6=0\Leftrightarrow-x+7=0\Leftrightarrow x=7\)

Bài 4: 

c) Ta có: \(\dfrac{x^3}{8}+\dfrac{x^2y}{2}+\dfrac{xy^2}{6}+\dfrac{y^3}{27}\)

\(=\left(\dfrac{x}{2}\right)^3+3\cdot\left(\dfrac{x}{2}\right)^2\cdot\dfrac{y}{3}+3\cdot\dfrac{x}{2}\cdot\left(\dfrac{y}{3}\right)^2+\left(\dfrac{y}{3}\right)^3\)

\(=\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^3\)

\(=\left(\dfrac{-1}{2}\cdot8+\dfrac{1}{3}\cdot6\right)^3=\left(-4+2\right)^3=-8\)

Bài 6:

a) Ta có: \(P=\left(x+2\right)^3+\left(x-2\right)^3-2x\left(x^2+12\right)\)

\(=x^3+6x^2+12x+8+x^3-6x^2+12x-8-2x^3-12x\)

=0

b) Ta có: \(Q=\left(x-1\right)^3-\left(x+1\right)^3+6\left(x+1\right)\left(x-1\right)\)

\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6x^2-6\)

=-8

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

6a.

$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$

$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$

Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

2:

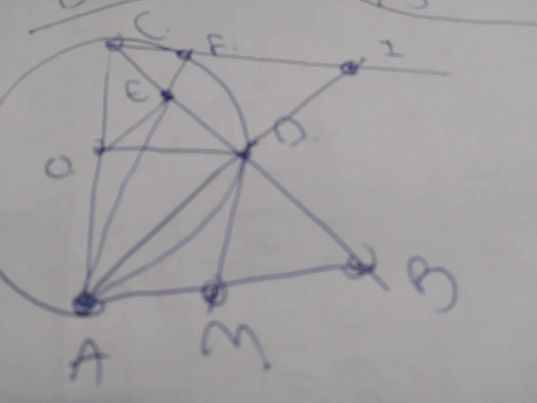
a: Xét tứ giác OAMD có

\(\widehat{OAM}+\widehat{ODM}=90^0+90^0=180^0\)

=>OAMD là tứ giác nội tiếp 

b: Xét (O) có

ΔADC nội tiếp 

AC là đường kính

Do đó: ΔADC vuông tại D

=>AD\(\perp\)BC tại D

Xét ΔABC vuông tại A có AD là đường cao

nên \(AD^2=DB\cdot DC\)

Xét (O) có

MA,MD là tiếp tuyến

Do đó: MA=MD

=>\(\widehat{MAD}=\widehat{MDA}\)

mà \(\widehat{MAD}+\widehat{MBD}=90^0\)(ΔADB vuông tại D)

và \(\widehat{MDA}+\widehat{MDB}=\widehat{BDA}=90^0\)

nên \(\widehat{MDB}=\widehat{MBD}\)

=>MD=MB

mà MD=MA

nên MB=MA

=>M là trung điểm của AB

Xét ΔABC có

M,O lần lượt là trung điểm của AB,AC

=>MO là đường trung bình

=>MO//BC

Bài III.2b.

Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)

hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)

\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có : 

\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)

\(=m^2+2m+1-4m-16\)

\(=m^2-2m-15>0\).

\(\Rightarrow m< -3\) hoặc \(m>5\).

Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)

\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)

\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)

Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).

Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)

Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)

\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).

Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).

Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt : 

\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)

Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).

Vậy : Không có giá trị m thỏa mãn đề bài.

Bài IV.b.

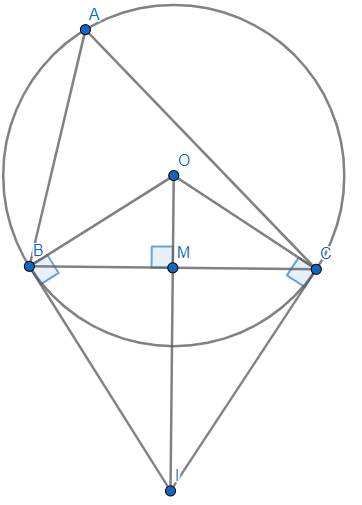
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).

Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).

Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).

Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).

Lại có : \(BC=MB+MC=2MB\)

\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)

Tính diện tích hình quạt tròn

Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).

\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)

Bài 4: 

b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK

nên \(BD\cdot BK=BA^2\left(1\right)\)

Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(BH\cdot BC=AB^2\left(2\right)\)

Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

III

1 It's colder today than yesterday

2 It takes 4 hours to travel by car and fives hours by train

3 We were busier at work today than everyday

4 Jane's sister cooks worse than her

5 Nobody in this team can play football as well as Tom

IV

1 D
2 A

4:

d: