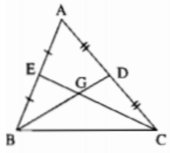
Gọi G là giao điểm của BD và CE.

Trong ∆GBC, ta có:

GB + GC > BC (bất đẳng thức tam giác)

GB = 2/3 BD (tính chất đường trung tuyến)

GC = 2/3 CE (tính chất đường trung tuyến)

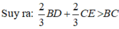
Mà BC = 10 cm (gt)

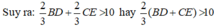
⇒ BD + CE > 15 (cm).

Ai giúp mình với mình sắp phải nộp bài rồi

bài này là bài 94 nâng cao và các chuyên đề toán 7

gọi G là giao điểm của BD và CE

=>G là trọng tâm cua tam giac ABC

=>GB=2/3 BD=6,GC=2/3CE=8

ta có GB^2+GC^2=6^2+8^2=100

màBC^2=10^2=100

nênGB^2+GC^2=BC^2

=>tam giac GBC vuong tai G(dinh li py ta go dao)

=> đpcm

Giải:
Gọi giao điểm giữa BD và CE là G

Ta có: \(GC=\dfrac{2}{3}EC\)

\(GB=\dfrac{2}{3}BD\)

\(\Rightarrow GC+GB=\dfrac{2}{3}EC+\dfrac{2}{3}BD\)

\(\Rightarrow GC+GB=\dfrac{2}{3}\left(EC+BD\right)\)

Mà \(GC+GB>BC\)

\(\Rightarrow\dfrac{2}{3}\left(EC+BD\right)>BC=10\left(cm\right)\)

\(\Rightarrow EC+BD>15\left(cm\right)\left(đpcm\right)\)

Vậy...

Gọi G là giao điểm của BD và CE. Theo bất đẳng thức trong tam giác GBC:

GB + GC > BC = 10 cm

\(\Rightarrow\dfrac{2}{3}BD+\dfrac{2}{3}CE>10cm\)

\(\Rightarrow BD+CE>\dfrac{3}{2}.10cm=15\left(cm\right)\).

Gọi giao điểm của BD và CE là G

=>G là trọng tâm của ΔABC

=>BG=2/3BD; CG=2/3CE

BG+CG>BC

hay BG+CG>10

=>2/3(BD+CE)>10

=>BD+CE>15