Gọi G là giao điểm của BD và CE.
Trong ∆GBC, ta có:
GB + GC > BC (bất đẳng thức tam giác)
GB = 2/3 BD (tính chất đường trung tuyến)
GC = 2/3 CE (tính chất đường trung tuyến)
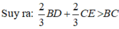
Mà BC = 10 cm (gt)
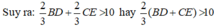
⇒ BD + CE > 15 (cm).
Gọi G là giao điểm của BD và CE.
Trong ∆GBC, ta có:
GB + GC > BC (bất đẳng thức tam giác)
GB = 2/3 BD (tính chất đường trung tuyến)
GC = 2/3 CE (tính chất đường trung tuyến)
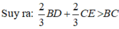
Mà BC = 10 cm (gt)
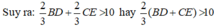
⇒ BD + CE > 15 (cm).
Tam giác ABC có BC=10cm,các đường trung tuyến BD và CE. Chứng minh rằng BD+CE > 15cm.
tam giac ABC có BC=10cm các đường trung tuyến BD và CE , chứng minh BD+CE>15cm
bài 1
cho tam giác ABC có BC=10cm, các đường trung tuyến BD và CE.Chứng minh rằng: BD + CE > 15cm
Cho tam giác ABC có BC = 10cm. Các đường trung tuyến BD và CE có độ dài theo thứ tự bằng 9cm và 12 cm. Chứng minh rằng: BD ⊥ CE
tam giác ABC có BC = 10cm, các đường trug tuyến BD và CE . Chứng minh rằng BD+CE>15 cm
Tam giác ABC, có BC=10cm. Các đường trung tuyến BD và CE có độ dài theo thứ tự bằng 9cm và 12cm. Chứng minh rằng BD vuông góc vs CE
1 / Cho tam giác ABC có BC = 10cm . Các đường trung tuyến BD và CE có độ dài theo thứ tự là 9cm và 12cm .Cm : BD vuông góc CE
2 / Cho tam giác ABC ,đường trung tuyến BD . Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi M và N lần lượt là trung điểm của BC và CE . Gọi I , K theo thứ tự giao điểm của AM , AN với BE . Chứng minh rằng : BI = IK = KE
Cho tam giác ABC có các đường trung tuyến AM BD và CE biết AB = 8 cm AC= 10 cm và BC = 14 cm chứng minh rằng BD+CE>24cm
cho tam giác ABC có BC=8, các đường trung tuyến BD,CE cắt nhau taih G. Chứng minh rằng BD+CE>12cm