giải phương trình
I 5x-1I -2x =7
Bài 3: Giải các phương trình sau bằng cách đưa về dạng ax +b =0 ( giải chi tiết )
a)7 – x = -2x +3
b) 2 (3x +1) = -2x +5
c) 5x + 2(x – 1) = 4x + 7.
d) 10x^2 - 5x(2x + 3) = 15
a: =>-x+2x=3-7
=>x=-4
b: =>6x+2+2x-5=0
=>8x-3=0
hay x=3/8
c: =>5x+2x-2-4x-7=0
=>3x-9=0
hay x=3
d: =>10x2-10x2-15x=15
=>-15x=15
hay x=-1
Giải phương trình: (2x + 7)(x - 5)(5x + 1) = 0
(2x + 7)(x – 5)(5x + 1) = 0
⇔ 2x + 7 = 0 hoặc x – 5 = 0 hoặc 5x + 1 = 0
+ 2x + 7 = 0 ⇔ 2x = -7 ⇔ 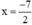
+ x – 5 = 0 ⇔ x = 5.
+ 5x + 1 = 0 ⇔ 5x = -1 ⇔ 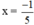
Vậy phương trình có tập nghiệm 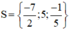
giải phương trình :
1) -2(x - 3) + 5x (x - 1) = 5x (x + 1)
2) 7 - (2x + 4) = -(x + 4)
1) -2(x - 3) + 5x (x - 1) = 5x (x + 1)
<=> -2x + 6 + 5x2 - 5x = 5x2 + 5x
<=> 6 = 5x2 + 5x + 2x - 5x2 + 5x
<=> 6 = 12x
<=> \(\dfrac{6}{12}\) = x = 0,5
vậy tập nghiệm S ={0,5}
2) 7 - (2x + 4) = -(x + 4)
<=> 7 - 2x - 4 = -x - 4
<=> 7 - 4 + 4 = -x + 2x
<=> 7 = x
vậy tập nghiệm S ={7}
3 √(2x + 7) + √(1 - 5x) + 2x^2+x-14=0
(giải phương trình)
Giải phương trình
1) (3x - 2)( 4x + 5) = 0
2) 2x - 7= 5x + 20
(3x-2)(4x+5)=0
=> 3x-2=0 hoặc 4x+5=0
3x=2 4x=-5
x=2/3 x=-5/4
2) 2x-7=5x+20
2x-5x=20+7
-3x=27
x=-9
Bài 1:
\(\Leftrightarrow3x-2=0\) hay \(\Leftrightarrow4x+5=0\)
\(\Leftrightarrow3x=2\) \(\Leftrightarrow4x=-5\)
\(\Leftrightarrow x=\dfrac{2}{3}\) \(\Leftrightarrow x=-\dfrac{5}{4}\)
Vậy S = \(\left\{\dfrac{2}{3};-\dfrac{5}{4}\right\}\)
Bài 2:
\(\Leftrightarrow2x-5x=20+7\\ \Leftrightarrow-3x=27\\ \Leftrightarrow x=\dfrac{27}{-3}=-9\)
Vậy S = -9
Giải các phương trình sau: 2x –(5x + 3) = 4(3x – 1) -7.
2x –(5x + 3) = 4(3x – 1) -7 ⇔ 2x – 5x – 3 = 12x- 4 – 7 ⇔ - 15x = -8 ⇔ x = 8/15
Vậy phương trình có nghiệm x = 8/15.
Bài 3: Giải các phương trình sau bằng cách đưa về dạng ax +b =0
a)7 – x = -2x +3
b) 2 (3x +1) = -2x +5
c) 5x + 2(x – 1) = 4x + 7.
d) 10x^2 - 5x(2x + 3) = 15
\(\)
a, <=> x = -4
b, <=> 6x + 2 = -2x + 5 <=> 8x = 3 <=> x = 3/8
c, <=> 5x + 2x - 2 = 4x + 7 <=> 2x = 9 <=> x = 9 /2
d, <=> 10x^2 - 10x^2 - 15x = 15 <=> x = -1
a, <=> x = -4
b, <=> 6x + 2 = -2x + 5 <=> 8x = 3 <=> x = 3/8
c, <=> 5x + 2x - 2 = 4x + 7 <=> 2x = 9 <=> x = 9 /2
d <=> 10x^2 - 10x^2 - 15x = 15 <=> x = -1
a) x=-4
b)4x=3
x=3/4
c)3x=9
x=3
d) 15x=15
x=1
Giải phương trình sau :
a,\(\dfrac{7-3x}{12}+\dfrac{5x+2}{7}=x+13\)
b,\(\dfrac{3\left(x+3\right)}{4}-\dfrac{1}{2}=\dfrac{5x+9}{7}-\dfrac{7x-9}{4}\)
c,\(\dfrac{2x+1}{3}-\dfrac{5x+2}{7}=x+3\)
d,\(\dfrac{2x-3}{3}-\dfrac{2x+3}{7}=\dfrac{4x+3}{5}-17\)
a: \(\Leftrightarrow7\left(7-3x\right)+12\left(5x+2\right)=84\left(x+13\right)\)
\(\Leftrightarrow49-21x+60x+24=84x+1092\)
\(\Leftrightarrow39x-84x=1092-73\)
=>-45x=1019
hay x=-1019/45
b: \(\Leftrightarrow21\left(x+3\right)-14=4\left(5x+9\right)-7\left(7x-9\right)\)
=>21x+63-14=20x+36-49x+63
=>21x+49=-29x+99
=>50x=50
hay x=1
c: \(\Leftrightarrow7\left(2x+1\right)-3\left(5x+2\right)=21x+63\)
=>14x+7-15x-6-21x-63=0
=>-22x-64=0
hay x=-32/11
d: \(\Leftrightarrow35\left(2x-3\right)-15\left(2x+3\right)=21\left(4x+3\right)-17\cdot105\)
=>70x-105-30x-45=84x+63-1785
=>40x-150-84x+1722=0
=>-44x+1572=0
hay x=393/11
a, msc 12.7=84
Chuyển vế về =0 rồi làm
b,msc 28
c,làm tương tự
a, \(\Rightarrow49-21x+60x+24=84x+1092\)
\(\Leftrightarrow-45x=1019\Leftrightarrow x=-\dfrac{1019}{45}\)
b, \(\Rightarrow21\left(x+3\right)-14=4\left(5x+9\right)-7\left(7x-9\right)\)
\(\Leftrightarrow21x+63-14=20x+36-49x+63\)
\(\Leftrightarrow50x=50\Leftrightarrow x=1\)
c, \(\Rightarrow14x+7-15x-6=21x+63\Leftrightarrow-22x=62\Leftrightarrow x=-\dfrac{31}{11}\)
d, \(\Rightarrow35\left(2x-3\right)-15\left(2x+3\right)=21\left(4x+3\right)-105.17\)
\(\Leftrightarrow70x-105-30x-45=84x+63-1785\)
\(\Leftrightarrow-44x=-1572\Leftrightarrow x=\dfrac{393}{11}\)
Giải các phương trình:
a) (x - 7)(2x + 8) = 0
b) (3x +1)(5x - 2) = 0
c) (x - 1)(2x + 7)(x2 + 2) = 0
d) (2x - 1)(x + 8)(x - 5) = 0
a) (x - 7)(2x + 8) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x-7=0\\2x+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\2x=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-4\end{matrix}\right.\)
Vậy: S = {7; -4}
b) Tương tự câu a
c) (x - 1)(2x + 7)(x2 + 2) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\\x^2+2=0\end{matrix}\right.\)
Mà: x2 + 2 > 0 với mọi x
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{1;-\dfrac{7}{2}\right\}\)
d) (2x - 1)(x + 8)(x - 5) = 0
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x+8=0\\x-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=1\\x=-8\\x=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-8\\x=5\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{1}{2};-8;5\right\}\)
a/ Pt \(\Leftrightarrow\left[{}\begin{matrix}x-7=0\\2x+8=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-4\end{matrix}\right.\)
Vậy \(S=\left\{7;-4\right\}\)
b/ pt \(\Leftrightarrow\left[{}\begin{matrix}3x+1=0\\5x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=\dfrac{2}{5}\end{matrix}\right.\)
c/ pt \(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\) (\(x^2+2>0\forall x\))\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)
d/ pt \(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x+8=0\\x-5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-8\\x=5\end{matrix}\right.\)
a)(x-7)(2x+8)=0
⇔x-7=0 hoặc 2x+8=0
1.x-7=0⇔x=7
2.2x+8=0⇔2x=-8⇔x=-4
phương trình có 1 nghiệm x=7 và x=-4
b)(3x+1)(5x-2)=0
⇔3x+1=0 hoặc 5x-2=0
1.3x+1=0⇔3x=-1⇔x=-1/3
2.5x-2=0⇔5x=2⇔x=5/2
phương trình có 2 nghiệm x=-1/3 và x=5/2