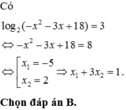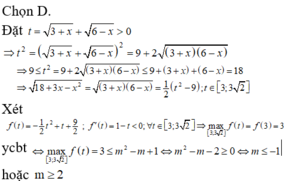x2-3x-18 ???

Những câu hỏi liên quan
Gọi
x
1
;
x
2
(
x
1
x
2
)
là hai giá trị thỏa mãn
x
2
+
3
x
–
18
0
. Khi đó
x...
Đọc tiếp
Gọi x 1 ; x 2 ( x 1 > x 2 ) là hai giá trị thỏa mãn x 2 + 3 x – 18 = 0 . Khi đó x 1 x 2 bằng
A. -2
B. 2
C. 1 2
D. - 1 2
Ta có
x 2 + 3 x – 18 = 0 ⇔ x 2 + 6 x – 3 x – 18 = 0 ⇔ ( x 2 – 3 x ) + ( 6 x – 18 ) = 0
ó x(x – 3) + 6(x – 3) = 0
ó (x + 6)(x – 3) = 0
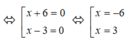
Suy ra x 1 = 3 ; x 2 = - 6 ( d o x 1 > x 2 )
=> x 1 x 2 = 3 - 6 = - 1 2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Gọi
x
1
,
x
2
x
1
x
2
là hai nghiệm của phương trình
log
2
-
x
2
-
3
x
+...
Đọc tiếp
Gọi x 1 , x 2 x 1 < x 2 là hai nghiệm của phương trình log 2 - x 2 - 3 x + 18 = 3 Giá trị x 1 + 3 x 2 bằng
A. -13
B. 1
C. 13
D. -1
Bài 1. Phân tích các đa thức sau thành nhân tử:a. 12x3y – 24x2y2 + 12xy3 b. x2 - 2xy – x2 + 4y2c. x2 – 2x - 4y2 + 1d. x2 + 3x – 18 e. x2 – 6 x +xy - 6yf. x2 + 2x + 1 - 16 g. x2 – 2x -3h. x2 - 8x +15 i. 2x2 + 2xy - x - y j. x2 - 4x + 4 - 25y2k. x2 + 4x -12 l. x2 + 6x +8m. ax – 2x - a2 +2an. x2 - 6xy + 9y2 -25z2o. x2 + x – 6 p. x2 -7 x + 6q. x3- 3x2 + 3x...
Đọc tiếp
Bài 1. Phân tích các đa thức sau thành nhân tử:
a. 12x3y – 24x2y2 + 12xy3 | b. x2 - 2xy – x2 + 4y2 | c. x2 – 2x - 4y2 + 1 | d. x2 + 3x – 18 |
e. x2 – 6 x +xy - 6y | f. x2 + 2x + 1 - 16 | g. x2 – 2x -3 | h. x2 - 8x +15 |
i. 2x2 + 2xy - x - y | j. x2 - 4x + 4 - 25y2 | k. x2 + 4x -12 | l. x2 + 6x +8 |
m. ax – 2x - a2 +2a | n. x2 - 6xy + 9y2 -25z2 | o. x2 + x – 6 | p. x2 -7 x + 6 |
q. x3- 3x2 + 3x -1 | r. 81 – x2 + 4xy – 4y2 | s. x2 -5x -6 | t. 3x2 - 7x + 2 |
u. 3x2 - 3y2 - 12x – 12y | v. x2 +6x –y2 +9 | w. x2 - 8 x – 9 | x. x4 + 64 |
b: \(=\left(x-y\right)^2-4y^2\)
\(=\left(x-y-2y\right)\left(x-y+2y\right)\)
\(=\left(x-3y\right)\left(x+y\right)\)
c: \(=x\left(x-6\right)+y\left(x-6\right)\)
\(=\left(x-6\right)\left(x+y\right)\)
Đúng 0
Bình luận (0)
phân tích các đa thức thành nhân tử
a) ( x2 + 4)2- 16x2
b) ( x+3)2- 8x3
c) (4x2-3x -18)2- ( 4x2 + 3x)2
\(a,\left(x^2+4\right)^2-16x^2=\left(x^2+4\right)-\left(4x\right)^2=\left(x^2+4-4x\right).\left(x^2+4+4x\right)=\left(x-2\right)^2.\left(x+2\right)^2\)
\(b,\left(x+3\right)^3-8x^3=\left(x+3\right)^3-\left(2x\right)^3=\left(x+3-2x\right).\left[x^2+\left(x+3\right).2x+\left(2x\right)^2\right]=\left(3-x\right).\left(x^2+2x^2+6x+4x^2\right)\)
\(c,\left(4x^2-3x-18\right)^2-\left(4x^2+3x\right)^2=\left(4x^2-3x-18-4x^2-3x\right).\left(4x^2-3x-18+4x^2+3x\right)=\left(-6x-18\right).\left(8x^2-18\right)\)
Đúng 0
Bình luận (0)
cho đa thức A=x2-5xy+5y2-3x+18 và B=-x2+3xy-y2-x-7 Biết A-C=B Tính giá trị của đa thức C khi x-y=4
C=A+B
=>C=(x2-5xy+5y2-3x+18y)-(-x2+3xy-y2-x-7)
=>C=x2-5xy+5y2-3x+18y+x2-3xy+y2+x+7
=>C=(x2+x2)-(5xy+3xy)+(5y2+y2)-(3x-x)+18y+7
=>C=2x2+6y2-8xy-2x+18y+7
tính giá trị C khó quá nên mình làm có đc 1 nửa thôi, sorry nha
Đúng 1
Bình luận (0)
tham khảo
C=A+B
=>C=(x2-5xy+5y2-3x+18y)-(-x2+3xy-y2-x-7)
=>C=x2-5xy+5y2-3x+18y+x2-3xy+y2+x+7
=>C=(x2+x2)-(5xy+3xy)+(5y2+y2)-(3x-x)+18y+7
=>C=2x2+6y2-8xy-2x+18y+7
Đúng 1
Bình luận (0)
Giải PT, a 4x+2=3x+1 ,b 6+2x=18-x C x2-6/x = x+3/2
a: =>4x-3x=1-2
=>x=-1
b: =>3x=12
=>x=4
c: =>2(x^2-6)=x(x+3)
=>2x^2-12-x^2-3x=0
=>x^2-3x-12=0
=>\(x=\dfrac{3\pm\sqrt{57}}{2}\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
3
x
+
1
+
6
x
-
1
-
18
+
3
x
-
x
2
≤
m
2
-
m
+
1
nghiệm đúng
∀...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 3 x + 1 + 6 x - 1 - 18 + 3 x - x 2 ≤ m 2 - m + 1 nghiệm đúng ∀ x ∈ - 3 ; 6 ?
A. m ≥ - 1 .
B. - 1 ≤ m ≤ 0 .
C. 0 ≤ m ≤ 2 .
D. m ≤ - 1 hoặc m ≥ 2 .
Gọi S là tập nghiệm của phương trình
5
x
2
+
4
x
−
x
2
−
3
x
−
18
5
x
. Số phần tử của S là: A. 1 B. 4 C. 3 D. 2
Đọc tiếp
Gọi S là tập nghiệm của phương trình 5 x 2 + 4 x − x 2 − 3 x − 18 = 5 x . Số phần tử của S là:
A. 1
B. 4
C. 3
D. 2
5 x 2 + 4 x − x 2 − 3 x − 18 = 5 x 1
ĐK: 5 x 2 + 4 x ≥ 0 x 2 − 3 x − 18 ≥ 0 x ≥ 0 ⇔ x ≥ 0 , x ≤ − 4 5 x ≥ 6 , x ≤ − 3 x ≥ 0 ⇔ x ≥ 6
Khi đó 1 ⇔ 5 x 2 + 4 x = 5 x + x 2 − 3 x − 18
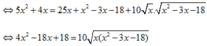
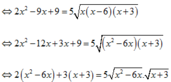
Dễ thấy x = 6 không là nghiệm phương trình nên với x > 6 ta chia cả hai vế cho x 2 − 6 x > 0 ta được:
2 + 3. x + 3 x 2 − 6 x = 5. x + 3 x 2 − 6 x 2
Đặt x + 3 x 2 − 6 x = t > 0 thì (2) trở thành 3 t 2 − 5 t + 2 = 0 ⇔ t = 1 ( T M ) t = 2 3 ( T M )
+ Nếu t = 1 thì x + 3 = x 2 − 6 x
⇔ x + 3 = x 2 − 6 x ⇔ x 2 − 7 x − 3 = 0 ⇔ x = 7 + 61 2 ( T M ) x = 7 − 61 2 ( L )
+ Nếu t = 2 3 thì x + 3 = 2 3 x 2 − 6 x ⇔ x + 3 = 4 9 ( x 2 − 6 x )
⇔ 4 x 2 − 33 x − 27 = 0 ⇔ x = 9 ( T M ) x = − 3 4 ( L )
Vậy phương trình đã cho có tập nghiệm s = 7 + 61 2 ; 9 hay S có 2 phần tử.
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Bài 2: Phân tích thành nhân tử:b) (x+2)2-25c) 36(x-y)2d) x2+1/2x+1/16e) 2x4y3-3x2y4+5x3y4f) 3x(x-2)+5(2-x)g) 3x(x-2y)+6y(2y-x)i) x(x-1)+(1-x)2k) 2y(x+2)-3x-6l) x2+6x-3(x+6)m) xy+x-2y-2n) 3x2-3xy-5x+5y15) x3-8/12516) x2-x-y2-yy17) x3+4x-(y3+4y)18) 5x-√5x+1/419) x3+2x2+x-16xy220) (x+2y)2-(x-y)21) (9x2-33x3x+2y+-4y222) 9x2-6xy+3x-y+y2
Đọc tiếp
Bài 2: Phân tích thành nhân tử:
b) (x+2)2-25
c) 36(x-y)2
d) x2+1/2x+1/16
e) 2x4y3-3x2y4+5x3y4
f) 3x(x-2)+5(2-x)
g) 3x(x-2y)+6y(2y-x)
i) x(x-1)+(1-x)2
k) 2y(x+2)-3x-6
l) x2+6x-3(x+6)
m) xy+x-2y-2
n) 3x2-3xy-5x+5y
15) x3-8/125
16) x2-x-y2-yy
17) x3+4x-(y3+4y)
18) 5x-√5x+1/4
19) x3+2x2+x-16xy2
20) (x+2y)2-(x-y)
21) (9x2-33x3x+2y+-4y2
22) 9x2-6xy+3x-y+y2
\(b,\left(x+2\right)^2-25\)
\(=\left(x+2\right)^2-5^2\)
\(=\left(x-3\right)\left(x+7\right)\)
\(c,36\left(x-y\right)^2\)
\(=36\left(x^2-2xy+y^2\right)\)
\(=36x^2-72xy+36y^2\)
\(d,x^2+\dfrac{1}{2}x+\dfrac{1}{16}\)
\(=x^2+2.x.\dfrac{1}{4}+\dfrac{1}{4}^2\)
\(=\left(x+\dfrac{1}{4}\right)^2\)
\(e,2x^4y^3-3x^2y^4+5x^3y^4\)
\(=x^2y^3\left(2x^2-3y+5xy\right)\)
Các câu còn lại làm tương tự, chú ý sd HĐT
Đúng 1
Bình luận (1)