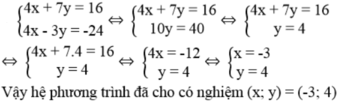Giải hệ phương trình (bằng phương pháp cộng đại số):

Những câu hỏi liên quan
giải hệ phương trình ( bằng phương pháp cộng đại số)
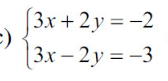
\(\left\{{}\begin{matrix}3x+2y=-2\\3x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+2y=-2\\3x+2y-3x+2y=-2+3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+2y=-2\\4y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+2.\dfrac{1}{4}=-2\\y=\dfrac{1}{4}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{6}\\x=\dfrac{1}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
giải hệ phương trình ( bằng phương pháp cộng đại số)
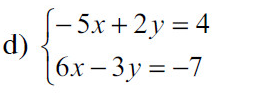
\(\left\{{}\begin{matrix}-5x+2y=4\\6x-3y=-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}15x-6y=-12\\12x-6y=-14\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}15x-6y=-12\\15x-6y-12x+6y=-12-\left(-14\right)\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}15x-6y=-12\\3x=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}15.\dfrac{2}{3}-6y=-12\\x=\dfrac{2}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{11}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(\Leftrightarrow\left\{{}\begin{matrix}15x-6y=-12\\12x-6y=-14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=2\\-5x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\2y-\dfrac{10}{3}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{11}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giải hệ phương trình ( bằng phương pháp cộng đại số)
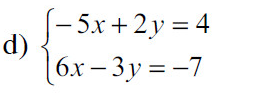
Giải hệ phương trình (bằng phương pháp cộng đại số).
Đọc tiếp
Giải hệ phương trình (bằng phương pháp cộng đại số).
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=10\\5x+2y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3x-5=4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải hệ phương trình (bằng phương pháp cộng đại số). a
Đọc tiếp
Giải hệ phương trình (bằng phương pháp cộng đại số). a
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-1\\x-2y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
Đúng 1
Bình luận (0)
Cho hệ phương trình: 3x-2y=4 (d1)
2x+y=5 (d2)
a) Giải hệ phương trình bằng phương pháp thế?
b) Giải hệ phương trình bằng phương pháp cộng đại số?
c) Vẽ (d1);(d2) trên cùng 1 mặt phẳng toạ độ. Xác định toạ độ giao điểm của d1 và d2
b: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-6\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=5-2x=5-12=-7\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
,
3
x
+
4
,
2
y
1
9
x
+
14...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3 , 3 x + 4 , 2 y = 1 9 x + 14 y = 4
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
3
x
-
2
y
10
x
-
2
3
y
3...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 3 x - 2 y = 10 x - 2 3 y = 3 1 3
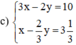 (Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)
(Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)
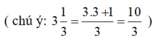
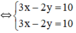 (Trừ từng vế hai phương trình)
(Trừ từng vế hai phương trình)
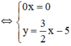
Phương trình 0x = 0 nghiệm đúng với mọi x.
Vậy hệ phương trình có vô số nghiệm dạng 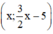 (x ∈ R).
(x ∈ R).
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
4
x
+
7
y
16
4
x
-
3
y
-
24
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 4 x + 7 y = 16 4 x - 3 y = - 24