Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy cho 2 điểm A(1;1) B (-2;4) . Tìm tọa độ điểm M trên trục Ox sao cho giá trị tuyệt đối vectơ MA -2 vectơ MB đạt giá trị nhỏ nhất
A M(1;0) B M(-3;0) C M(7;0) D M(-5;0)
Xem chi tiết
Gọi \(M\left(m;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;1\right)\\\overrightarrow{MB}=\left(-2-m;4\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}-2\overrightarrow{MB}=\left(m+5;-7\right)\)
\(\Rightarrow\left|\overrightarrow{MA}-2\overrightarrow{MB}\right|=\sqrt{\left(m+5\right)^2+49}\ge7\)
Dấu "=" xảy ra khi \(m+5=0\Leftrightarrow m=-5\) hay \(M\left(-5;0\right)\)
Đúng 1
Bình luận (1)
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;-3) có vectơ pháp tuyến
n
→
(
2
;
-
1
;
3
)
là A. 2x - y + 3z + 9 0 B. 2x -y + 3z - 4 0 C. x - 2y - 4 0 D. 2x - y + 3z + 4 0
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi
qua điểm A(1;2;-3) có vectơ pháp tuyến n → = ( 2 ; - 1 ; 3 ) là
A. 2x - y + 3z + 9 = 0
B. 2x -y + 3z - 4 = 0
C. x - 2y - 4 = 0
D. 2x - y + 3z + 4 = 0
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;-3) có vectơ pháp tuyến n → = ( 2 ; - 1 ; 3 ) là
A. 2x - y + 3z + 9 = 0
B. 2x - y + 3z - 4 = 0
C. x - 2y - 4 = 0
D. 2x - y + 3z + 4
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+y-4z0, đường thẳng
d
:
x
-
1
2
y
+
1
-
1
z
-
3
1
và điểm A(1;3;1) thuộc mặt phẳng (P). Gọi ∆ là đường thẳng...
Đọc tiếp
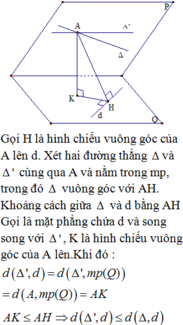
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+y-4z=0, đường thẳng d : x - 1 2 = y + 1 - 1 = z - 3 1 và điểm A(1;3;1) thuộc mặt phẳng (P). Gọi ∆ là đường thẳng đi qua A, nằm trong mặt phẳng (P) và cách d một khoảng cách lớn nhất. Gọi u → = a ; b ; 1 là một vectơ chỉ phương của đường thẳng ∆. Tính a+2b.
A. 7
B. -3
C. 0
D. 4
Trong mặt phẳng tọa độ,cho vectơ u=1/2 vectơ i -5 vectơ j và vectơ v=K vectơ i -4 vectơ j a)tìm các giá trị của K để | vectơ u|=| vectơ v| Giúp tui với mng
cho tam giác ABC có A<90 độ . M là trung điểm của BC .Dựng tam giác vuông cân BAD và CAE (C;Dcùng nửa mặt phẳng bờ AB ,B và E cùng nửa mặt phẳng bờ AC ).Chứng minh AM vuông góc với DE
ai giải được sẽ được mình tích
Trong mặt phẳng Oxy,cho hình bình hành ABCD có vectơ AC=(7;-3), vecto BD (-3;4).tìm tọa đọ của vecto AB
\(\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}=\overrightarrow{AC}-\overrightarrow{AB}-\overrightarrow{BD}\)
\(\Rightarrow2\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BD}\Rightarrow\overrightarrow{AB}=\frac{1}{2}\left(\overrightarrow{AC}-\overrightarrow{BD}\right)=\left(5;-\frac{7}{2}\right)\)
Trong mặt phẳng Oxy,cho hình bình hành ABCD có vectơ AC=(7;-3), vecto BD (-3;4).tìm tọa đọ của vecto AB
Áp dụng quy tắc hình bình hành ta có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AD}=\widehat{AC}\\\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{BD}\end{matrix}\right.\)
Từ hệ trên suy ra:
\(\overrightarrow{2AB}=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)-\left(\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{AC}-\overrightarrow{BD}\)
\(\Leftrightarrow\overrightarrow{AB}=\frac{1}{2}\left(\overrightarrow{AC}-\overrightarrow{BD}\right)=\frac{1}{2}\left[7-\left(-3\right);-3-4\right]=\left(5;\frac{-7}{2}\right)\)
Cho tam giác ABC có trực tâm H và nội tiếp đường tròn tâm O. Gọi B', A' lần lượt là điểm đối xứng với B và A qua O. M là trung điểm của BC
a) Cmr: Vectơ B'C = Vectơ AH
b) Cmr: Vectơ HM = Vectơ MA
c) AH cắt BC tại I và cắt (O) tại K. Cmr: Vectơ IH = Vectơ KI