Trên tia Ox cho 3 điểm A,B,C phân biệt. Chứng minh rằng:
a) Nếu OA+OB<OC thì B nằm giữa O và C
b) Nếu OA+AB+BC = OC thì điểm B nằm giữa hai điểm A và C
*giúp mjk với* T.T
Bài 2: (Vẽ hình) Cho \(\widehat{xOy}\). Trên tia \(Ox\) lấy điểm \(A\), trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA=OB\). Gọi \(C\) là 1 điểm trên tia phân giác \(Oz\) của \(\widehat{xOy}\). Chứng minh rằng:
a, \(AC=BC\)
\(\widehat{xAC}=\widehat{yBC}\)
b, \(OC=OB\)
`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`
Cho góc xOy. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA=OB. Gọi K là giao điểm của AB tới tia phân giác của góc xOy. Chứng minh rằng:
a) AK=KB b) OK vuông góc AB
a: ΔOAB cân tại O
mà OK là phân giác
nên K là trung điểm của AB
=>KA=KB
b: ΔOAB cân tại O
mà OK là phân giác
nên OK vuông góc AB
. Cho góc xOy = 1200
có Oz là tia phân giác. Trên Ox lấy điểm A, trên Oz lấy điểm B và trên
Oy lấy điểm C sao cho OA = OB = OC. Chứng minh rằng:
a) Tam giác OAB và tam giác OBC là tam giác đều
b) OA // CB, OC // AB
c) OB vuông góc với AC
vẽ hình giúp mik nha!!
Cho góc nhọn xoy trên ox lấy điểm A, B sao cho 0<OA<OB. Trên tia Oy lấy 2 điểm C, D
sao cho OA=OC, OB=OD. Gọi M là giao điểm của AD và BC, N là giao điểm của ON và BD. Chứng minh rằng:
a) △OAD bằng △OCB
b) △ADM bằng △CDM
c) OM là tia phân giác của góc xOy
d) ON ⊥ BD
a: Xét ΔOAD và ΔOCB có
OA=OC
góc O chung
OD=OB
=>ΔOAD=ΔOCB
b: Xét ΔMAB và ΔMCD co
góc MAB=góc MCD
AB=CD
góc MBA=góc MDC
=>ΔMAB=ΔMCD
c: ΔMAB=ΔMCD
=>MA=MC
Xét ΔOAM và ΔOCM co
OA=OC
AM=CM
OM chung
=>ΔOAM=ΔOCM
=>góc AOM=góc COM
=>OM là phân giác của góc BAC
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC
b) \(\Delta EAB=\Delta ECD\)
c) OE là tia phân giác của góc xOy.
Tham khảo:
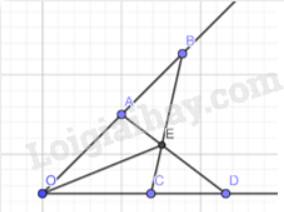
a) Xét \(\Delta OAD\) và \(\Delta OCB\), ta có :
OD = OB
\(\widehat{A}\) chung
OA = OC
\(\Rightarrow \Delta OAD=\Delta OCB\) (c-g-c )
\( \Rightarrow AD = BC\)(2 cạnh tương ứng )
b) Vì \(\Delta OAD=\Delta OCB\) nên \(\widehat{OAD}=\widehat{OCB}; \widehat{D}=\widehat{B}\) ( 2 góc tương ứng)
Mà \(\widehat{OAD}+\widehat{BAD}=180^0\) ( 2 góc kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) ( 2 góc kề bù)
Do đó, \(\widehat{BAD}=\widehat{BCD}\)
Vì \(OA+AB=OB; OC+CD=OD\)
Mà \(OC = OA, OD = OB\)
\(\Rightarrow AB=CD\)
Xét \(\Delta EAB\) và \(\Delta ECD\), ta có:
\(\widehat {ABE} = \widehat {CDE}\)
\(AB = CD\)
\(\widehat {BAE} = \widehat {DCE}\)
\(\Rightarrow \Delta EAB=\Delta ECD\) (g-c-g)
c) Vì \(\Delta EAB=\Delta ECD\) nên EB = ED ( 2 cạnh tương ứng)
Xét \(\Delta OBE\) và \(\Delta ODE\), ta có :
EB = ED
OB = OD
OE chung
\( \Rightarrow \Delta OBE=\Delta ODE \) (c.c.c)
\( \Rightarrow \widehat{BOE}=\widehat{DOE}\) ( 2 góc tương ứng)
\( \Rightarrow \) OE là phân giác \(\widehat {xOy}\)
Trên tia Ox cho ba điểm A,B,C phân biệt. Chứng minh rằng:
a.Nếu OA+OB<OC thì điểm B nằm giữa hai điểm O và C.
b.Nếu OA+AB+BC=OC thì điểm B nằm giữa hai điểm A và C.
BẠN THAM KHẢO Ở ĐÂY NHÉ
https://lazi.vn/edu/exercise/tren-tia-ox-cho-ba-diem-a-b-c-phan-biet-chung-minh-rang-a-neu-oa-ob-oc-thi-b-nam-giua-hai-diem-o-va-c
Trên tia ox lấy 3 điểm A,b,c sao cho OA=2cm , OB = 12cm , OC = 10cm a)So sánh OA và OC b)Gọi N là trung điểm của OB . Tính NC? c)Trên tia đối của tia Cx lấy điểm E sao cho CE = 2cm . Chứng minh : C là trung điểm của EB ? Cảm ơn nếu đã giúp mình :3
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.
Chứng minh rằng:
a) \(\Delta \)OAN = \(\Delta \)OBM;
b) \(\Delta \)AMN = \(\Delta \)BNM.
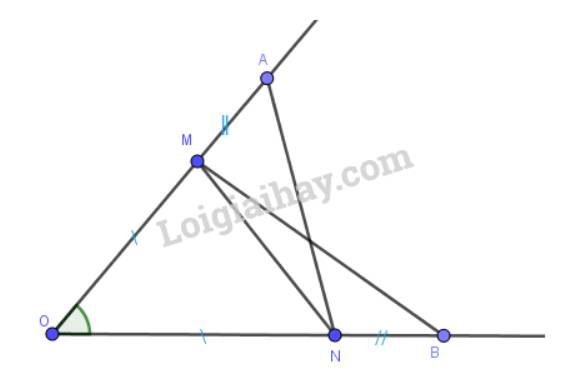
a) Xét \(\Delta OAN\) và \(\Delta OBM \) có:
OA=OB (gt)
\(\widehat{O}\) chung
OM=ON (gt)
=>\(\Delta OAN = \Delta OBM\)(c.g.c)
b) Do \(\Delta OAN = \Delta OBM\) nên AN=BM ( 2 cạnh tương ứng); \(\widehat {OAN} = \widehat {OBM}\)( 2 góc tương ứng) =>\(\widehat {NAM} = \widehat {MBN}\)
Do OA + AM = OM; OB + BN = ON
Mà OA = OB, OM =ON
=> AM=BN
Xét \(\Delta AMN\) và \(\Delta BNM\) có:
AN=BM (cmt)
\(\widehat {NAM} = \widehat {MBN}\) (cmt)
AM=BN (cmt)
=>\(\Delta AMN = \Delta BNM\)(c.g.c)
Cho góc xOy kkhác góc bẹt, tia phân giác Ot. Trên tia Ox lấy điểm A, Trên tia Oy lấy điểm B sao cho OA=OB.
a) Chứng minh Ot vuông góc AB
b) Trên tia Ot lấy điểm C , OC lớn hơn OB . Chứng minh Co là tia phân giác góc BCA và CB = CA.
a: Gọi H là một điểm bất kỳ trên tia Ot
Xét ΔOAB có OA=OB
nên ΔOAB cân tại O
mà OH là tia phân giác ứng với cạnh AB
nên Ot là đường cao ứng với cạnh AB