\(\frac{x}{10}\)-\(\frac{1}{y}\)=\(\frac{3}{10}\)

Những câu hỏi liên quan
Vẽ các hypebol sau:
a) \(\frac{{{x^2}}}{{10}} - \frac{{{y^2}}}{6} = 1\)
b) \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
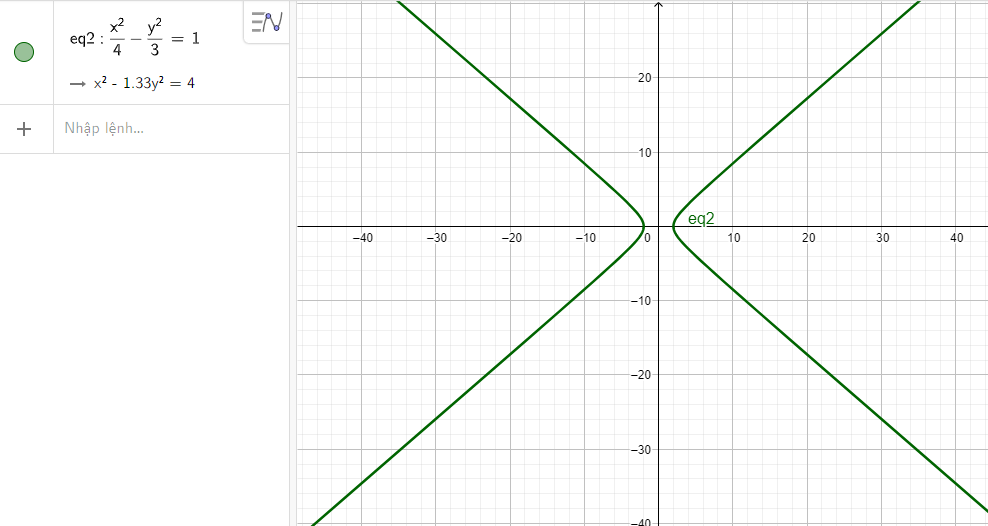
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Đúng 0
Bình luận (0)
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
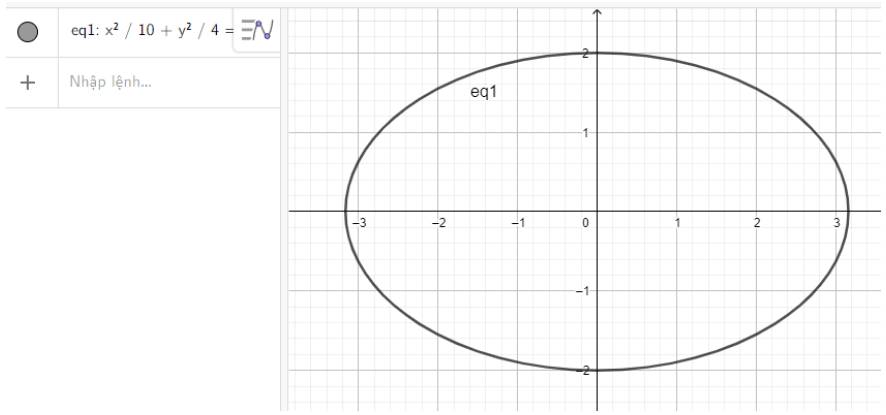
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
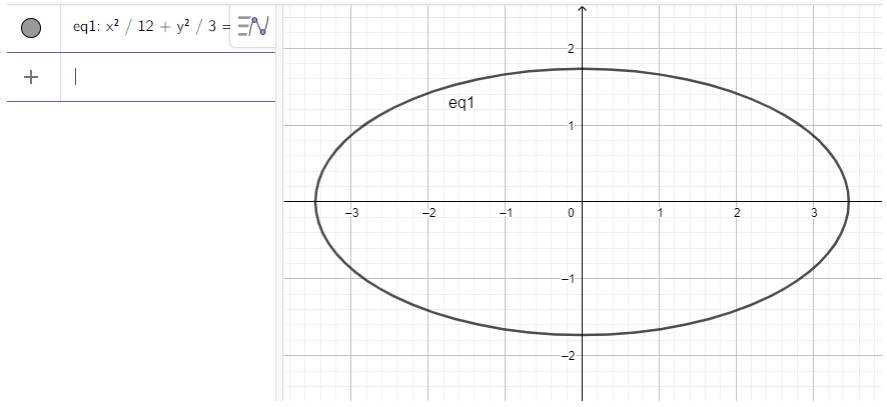
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
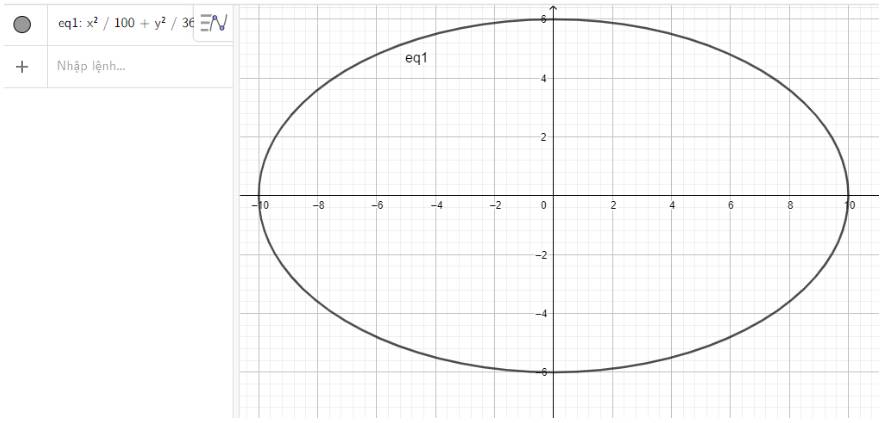
Đúng 0
Bình luận (0)
tìm x y biết : \(\frac{x}{10}-\frac{1}{y}=\frac{3}{10}\)
Bài 2
a) Tìm x biết\(\frac{1}{2}-\left|\frac{5}{4}-2x\right|=\frac{1}{3}\)
b) Tìm x biết \(\frac{x+1}{10}+\frac{x+1}{11}+\frac{x+1}{12}=\frac{x+1}{13}+\frac{x+1}{14}\)
c) Tìm ba số x, y, z thỏa mãn: \(\frac{x}{y}=\frac{10}{9};\frac{y}{z}=\frac{3}{4}\)và \(x-y+z=78\)
a) \(\frac{1}{2}-|\frac{5}{4}-2x|=\frac{1}{3}\Leftrightarrow|\frac{5}{4}-2x|=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{5}{4}-2x=\frac{1}{6}\\\frac{5}{4}-2x=-\frac{1}{6}\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=\frac{5}{4}-\frac{1}{6}=\frac{13}{12}\\2x=\frac{5}{4}+\frac{1}{6}=\frac{17}{12}\end{cases}}}\)
Tự làm nốt và kết luận
b) \(\frac{x+1}{10}+\frac{x+1}{11}+\frac{x+1}{12}=\frac{x+1}{13}+\frac{x+1}{14}\)
\(\Leftrightarrow\frac{x+1}{10}+\frac{x+1}{11}+\frac{x+1}{12}-\frac{x+1}{13}-\frac{x+1}{14}=0\)
\(\Leftrightarrow\left(x+1\right)\left(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}+\frac{1}{14}\right)=0\)
Vì \(\left(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}+\frac{1}{14}\right)\ne0\forall x\Rightarrow x+1=0\Leftrightarrow x=-1\)
Vậy ....
c) \(\frac{x}{y}=\frac{10}{9}\Leftrightarrow\frac{x}{10}=\frac{y}{9};\frac{y}{z}=\frac{3}{4}\Leftrightarrow\frac{y}{3}=\frac{z}{4}\Leftrightarrow\frac{y}{9}=\frac{x}{12}\)
\(\Leftrightarrow\frac{x}{10}=\frac{y}{9}=\frac{z}{12}\). Mà \(x-y+z=78\). Áp dụng t/c dãy tỉ số bằng nhau
\(\frac{x}{10}=\frac{y}{9}=\frac{z}{12}=\frac{x-y+z}{10-9+12}=\frac{78}{13}=6\)
\(\Rightarrow x=6.10=60;y=6.9=54;z=6.12=72\)
Vậy..........
tìm x,y thuộcZ sao cho
a,\(\frac{x}{10}-\frac{1}{y}=\frac{3}{10}\)
b,\(\frac{1}{x}+\frac{y}{2}=\frac{5}{8}\)
a,Ta có:x/10-1/y=3/10
=>1/y=x/10-3/10
1/y=x-3/10
=>y.(x-3)=1.10
Mà 10=1.10=2.5=-1.-10=-2.-5
Vì x,y thuộc Z =>Ta có bảng giá trị sau:
| x-3 | 1 | 10 | 2 | 5 | -1 | -10 | -2 | -5 |
| x | 4 | 13 | 5 | 8 | 2 | -7 | 1 | -2 |
| y | 10 | 1 | 5 | 2 | -10 | -1 | -5 | -2 |
(Câu kết luận cuối cùng bạn tự làm nhé,khi thay x,y vào phân số mình nghĩ bạn ko nên rút gọn nó nếu làm như vậy thì giá trị x,y sẽ bị thay đổi còn trường hợp x,y trùng nhau thì mình ko biết và x,y thẳng hàng nhau là 1 cặp x,y đừng lẫn sang cột khác nhek~)
b,1/x+y/2=5/8
Ta có:1/x=5/8-y/2
=>1/x= 5/8-4y/8
=>1/x=5-4y/8
=>x.(5-4y)=1.8
Mà 8=1.8=2.4=-1.-8=-2.-4
Vì x,y thuộc Z=>Ta có bảng giá trị sau:
| 5-4y | 1 | 8 | 2 | 4 | -1 | -8 | -2 | -4 |
| 4y | 4 | -3 | 3 | 1 | 6 | 13 | 7 | 9 |
| y | 1 | -3/4(loại vì y thuộc Z) | 3/4(loại vì y thuộc Z) | 1/4(loại vì y thuộcZ) | 3/2(loại vì y thuộc Z) | 13/4(loại vì y thuộc Z) | 7/4 (loại vì y thuộc Z) | 9/4(loại vì y thuộc Z) |
| x | 8 | 1 | 4 | 2 | -8 | -1 | -4 | -2 |
(Các chỗ mình viết thuộc bạn có thể viết kí hiêu cho nhanh nhek)(Các dấu. đó là nhân)
Đúng 0
Bình luận (0)
a) \(\frac{x}{10}-\frac{1}{y}=\frac{3}{10}\Rightarrow\frac{1}{y}=\frac{x}{10}-\frac{3}{10}\Rightarrow\frac{1}{y}=\frac{x-3}{10}\)
\(\Rightarrow y.\left(x-3\right)=10\Rightarrow y;x-3\inƯ\left(10\right)=\left\{1;2;5;10;-1;-2;-5;-10\right\}\)
Ta có bảng sau:
| \(x-3\) | \(1\) | \(10\) | \(2\) | \(5\) | \(-1\) | \(-10\) | \(-2\) | \(-5\) |
| \(x\) | \(4\) | \(13\) | \(5\) | \(8\) | \(2\) | \(-7\) | \(1\) | \(-2\) |
| \(y\) | \(10\) | \(1\) | \(5\) | \(2\) | \(-10\) | \(-1\) | \(-5\) | \(-2\) |
| Đánh giá | \(Đ\) | \(Đ\) | \(Đ\) | \(Đ\) | \(Đ\) | \(Đ\) | \(Đ\) | \(Đ\) |
Vậy \(\left(x;y\right)\in\left\{\left(4;10\right);\left(13;1\right);\left(5;5\right);\left(8;2\right);\left(2;-10\right);\left(-7;-1\right);\left(1;-5\right);\left(-2;-2\right)\right\}\)
b) \(\frac{1}{x}+\frac{y}{2}=\frac{5}{8}\Rightarrow\frac{1}{x}=\frac{5}{8}-\frac{y}{2}=\frac{5-4y}{8}\Rightarrow\frac{1}{x}=\frac{5-4y}{8}\)
\(\Rightarrow x.\left(5-4y\right)=8\Rightarrow x;\left(5-4y\right)\inƯ\left(8\right)=\left\{1;2;4;8;-1;-2;-4;-8\right\}\)
| \(x\) | \(1\) | \(8\) | \(2\) | \(4\) | \(-1\) | \(-8\) | \(-2\) | \(-4\) |
| \(5-4y\) | \(8\) | \(1\) | \(4\) | \(2\) | \(-8\) | \(-1\) | \(-4\) | \(-2\) |
| \(4y\) | \(-3\) | \(4\) | \(1\) | \(3\) | \(13\) | \(6\) | \(9\) | \(7\) |
| \(y\) | \(\frac{-3}{4}\) | \(1\) | \(\frac{1}{4}\) | \(\frac{3}{4}\) | \(\frac{13}{4}\) | \(\frac{3}{2}\) | \(\frac{9}{4}\) | \(\frac{7}{4}\) |
| Đánh giá | \(S\) | \(Đ\) | \(S\) | \(S\) | \(S\) | \(S\) | \(S\) | \(S\) |
Vậy \(x=8;y=1\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
\(\hept{\begin{cases}x+y+\frac{2}{x}+\frac{1}{y}=\frac{19}{3}\\xy+\frac{1}{xy}=\frac{10}{3}\end{cases}}\)
ĐKXĐ : \(x\ne0;y\ne0\)
Giải pt thứ 2 ta được
\(xy+\frac{1}{xy}=\frac{10}{3}\)
\(\Leftrightarrow\frac{\left(xy\right)^2+1}{xy}=\frac{10}{3}\)
\(\Leftrightarrow3\left(xy\right)^2+3=10xy\)
\(\Leftrightarrow3\left(xy\right)^2-10xy+3=0\)
\(\Leftrightarrow\left(xy-3\right)\left(3xy-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}xy=3\\xy=\frac{1}{3}\end{cases}}\left(TmĐK\right)\)
*Với \(xy=3\)
Giải pt (1) được
\(x+y+\frac{2}{x}+\frac{1}{y}=\frac{19}{3}\)
\(\Leftrightarrow x+y+\frac{2y+x}{xy}=\frac{19}{3}\)
\(\Leftrightarrow x+y+\frac{x+2y}{3}=\frac{19}{3}\)
\(\Leftrightarrow3x+3y+x+2y=19\)
\(\Leftrightarrow4x+5y=19\)
Ta có hệ mới \(\hept{\begin{cases}4x+5y=19\\xy=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{19-5y}{4}\\\frac{19-5y}{4}.y=3\left(#\right)\end{cases}}\)
Giải (#) được\(\left(#\right)\Leftrightarrow19y-5y^2=12\)
\(\Leftrightarrow5y^2-19y+12=0\)
\(\Leftrightarrow\left(y-3\right)\left(5y-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y=3\\y=\frac{4}{5}\end{cases}}\)
+) Với \(y=3\Rightarrow x=\frac{19-5y}{4}=\frac{19-5.3}{4}=1\)(Tm)
+) với \(y=\frac{4}{5}\Rightarrow x=\frac{19-5y}{4}=\frac{19-\frac{5.4}{5}}{4}=\frac{15}{4}\)(Tm)
Làm tương tự với trường hợp xy=1/3 nhé
Đúng 0
Bình luận (0)
bài 1: cho x, y thuộc Q. cmr:
|x + y| =< |x| + |y|
bài 2: tính:
\(A=\frac{\left(13\frac{1}{4}-2\frac{5}{27}-10\frac{5}{6}\right).230\frac{1}{25}+46\frac{3}{4}}{\left(1\frac{3}{7}+\frac{10}{3}\right):\left(12\frac{1}{3}-14\frac{2}{7}\right)}\)
bài 3: cho a + b + c = a^2 + b^2 + c^2 = 1 và x : y : z = a : b : c.
cmr: (x + y + z)^2 = x^2 + y^2 + z^2
1
fddfssdfdsfdssssssssssssssffffffffffffffffffsssssssssssssssssssfsssssssssssssssssssssssfffffffffffffff
Đúng 0
Bình luận (0)
Ez lắm =)
Bài 1:
Với mọi gt \(x,y\in Q\) ta luôn có:
\(x\le\left|x\right|\) và \(-x\le\left|x\right|\)
\(y\le\left|y\right|\) và \(-y\le\left|y\right|\Rightarrow x+y\le\left|x\right|+\left|y\right|\) và \(-x-y\le\left|x\right|+\left|y\right|\)
Hay: \(x+y\ge-\left(\left|x\right|+\left|y\right|\right)\)
Do đó: \(-\left(\left|x\right|+\left|y\right|\right)\le x+y\le\left|x\right|+\left|y\right|\)
Vậy: \(\left|x+y\right|\le\left|x\right|+\left|y\right|\)
Dấu "=" xảy ra khi: \(xy\ge0\)
Đúng 0
Bình luận (0)
Bài 3:
Ta có: \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x+y+z}{a+b+c}=x+y+z\) (vì a + b + c = 1)
Do đó: \(\left(x+y+z\right)^2=\frac{x^2}{a^2}=\frac{y^2}{b^2}=\frac{z^2}{c^2}=\frac{x^2+y^2+z^2}{a^2+b^2+c^2}=x^2+y^2+z^2\) (vì a2 + b2 + c2 = 1)
Vậy: (x + y + z)2 = x2 + y2 + z2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1.tìm các số x,y,z biết
a)frac{x}{y}frac{7}{13}và x+y60 b)frac{x}{y}frac{y}{10}frac{z}{6}và x+y+z92
c)frac{x}{y}frac{9}{10}và y-x120 d)frac{x}{2}frac{y}{3}frac{z}{4}và x+y+z81
e)frac{x}{4}frac{y}{12}frac{z}{15}và y-x4 f)frac{x}{3}frac{y}{4}và 2x+5y10
Đọc tiếp
1.tìm các số x,y,z biết
a)\(\frac{x}{y}=\frac{7}{13}\)và x+y=60 b)\(\frac{x}{y}=\frac{y}{10}=\frac{z}{6}và\) x+y+z=92
c)\(\frac{x}{y}=\frac{9}{10}và\) y-x=120 d)\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}và\) x+y+z=81
e)\(\frac{x}{4}=\frac{y}{12}=\frac{z}{15}và\) y-x=4 f)\(\frac{x}{3}=\frac{y}{4}và\) 2x+5y=10
1)
a) Ta có: \(\frac{x}{y}=\frac{7}{13}\).
=> \(\frac{x}{7}=\frac{y}{13}\) và \(x+y=60.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{x}{7}=\frac{y}{13}=\frac{x+y}{7+13}=\frac{60}{20}=3.\)
\(\left\{{}\begin{matrix}\frac{x}{7}=3=>x=3.7=21\\\frac{y}{13}=3=>y=3.13=39\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(21;39\right).\)
c) Ta có: \(\frac{x}{y}=\frac{9}{10}.\)
=> \(\frac{x}{9}=\frac{y}{10}\) và \(y-x=120.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{x}{9}=\frac{y}{10}=\frac{y-x}{10-9}=\frac{120}{1}=120.\)
\(\left\{{}\begin{matrix}\frac{x}{9}=120=>x=120.9=1080\\\frac{y}{10}=120=>y=120.10=1200\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(1080;1200\right).\)
d) Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}.\)
=> \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\) và \(x+y+z=81.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{81}{9}=9.\)
\(\left\{{}\begin{matrix}\frac{x}{2}=9=>x=9.2=18\\\frac{y}{3}=9=>y=9.3=27\\\frac{z}{4}=9=>z=9.4=36\end{matrix}\right.\)
Vậy \(\left(x;y;z\right)=\left(18;27;36\right).\)
Mình chỉ làm 3 câu thôi nhé, dài quá bạn.
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
\(\hept{\begin{cases}\frac{x+4}{x+3}-\frac{2}{y-1}=10\\\frac{x+6}{x+3}+\frac{1}{y-1}=7\end{cases}}\)
ta có : \(\hept{\begin{cases}1+\frac{1}{x+3}-2.\frac{1}{y-1}=10\\1+3.\frac{1}{x+3}+\frac{1}{y-1}=7\end{cases}}\)
gọi a=\(\frac{1}{x+3}\);b=\(\frac{1}{y-1}\) ta được
\(\hept{\begin{cases}1+a-2b=10\\1+3a+b=7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a-2b=9\\3a+b=6\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a=3\\b=-3\end{cases}}\)
thay a=\(\frac{1}{x+3}\)ta được:\(\frac{1}{x+3}=3\Rightarrow x=\frac{-8}{3}\)
tương tự y=\(\frac{2}{3}\)
vậy......
Cho hệ phương trình:\(\hept{\begin{cases}\frac{x}{3}+\frac{y}{12}-\frac{z}{4}=1\\\frac{x}{10}+\frac{y}{5}+\frac{z}{3}=1\end{cases}}\)Tính x+y+z
1 slot tối làm cho.Giờ đi học đã =))
Đúng 0
Bình luận (0)
\(\hept{\begin{cases}\frac{x}{3}+\frac{y}{12}-\frac{z}{4}=1\\\frac{x}{10}+\frac{y}{5}+\frac{z}{3}=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x+y-3z=12\\3x+6y+10z=30\end{cases}}\)
\(\Rightarrow7\left(x+y+z\right)=42\)
\(\Leftrightarrow x+y+z=6\)
Đúng 0
Bình luận (0)
\(\hept{\begin{cases}\frac{x}{3}+\frac{y}{12}-\frac{z}{4}=1\\\frac{x}{10}+\frac{y}{5}+\frac{z}{3}=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x+y-3z=12\\3x+6y+10z=30\end{cases}}\)
=> 7 ( x + y +z ) = 42
<=> x + y + z = 6
Đúng 0
Bình luận (0)
























